1、SAR ADC 采样精度与前端阻抗设计解析

说明：以下是从ADC的角度来描述的

一、定义

1. 输入阻抗

输入阻抗是指电路输入端对信号源（输出端）所呈现的阻抗。输入阻抗越高，信号源所需提供的电流越小，对信号源性能造成的影响也越小。在 ADC 采样和前端放大电路设计中，为了保持信号的稳定性和提高采样精度，通常希望 ADC 的输入阻抗尽可能高。

2. 输出阻抗

输出阻抗是指电路输出端（如传感器或前级放大器）对其负载（例如 ADC 输入端）所呈现的阻抗。输出阻抗越低，驱动负载的能力越强，电压下降越小，有助于信号的准确传输。理想情况下，输出阻抗应尽量小。

二、输入与输出阻抗的计算方法

1. 输入阻抗计算（以 ADC 为例）

ADC 的输入阻抗通常与其内部结构（如采样保持电容）以及采样时间设置密切相关。在芯片手册中通常可查到等效输入阻抗的估算值。

（1）测量方法：在 ADC 输入端加上一个已知电压 V i n V_{in} Vin​，测量流入的电流 I i n I_{in} Iin​，可通过以下公式估算输入阻抗： Z i n = V i n I i n （公式 1 ） Z_{in}=\frac{V_{in}}{I_{in}}（公式1） Zin​=Iin​Vin​​（公式1）

当使用如 STM32 等 MCU 的内部 ADC 时，也可以通过调整采样时间（Sample Time）来间接提高输入阻抗，减少前端电路负担。

（2)通过手册计算

暂无

2. 输出阻抗计算

输出阻抗同样可以通过公式1进行测量。在信号源输出电压前接入已知负载电阻并测其压降来间接估算输出阻抗

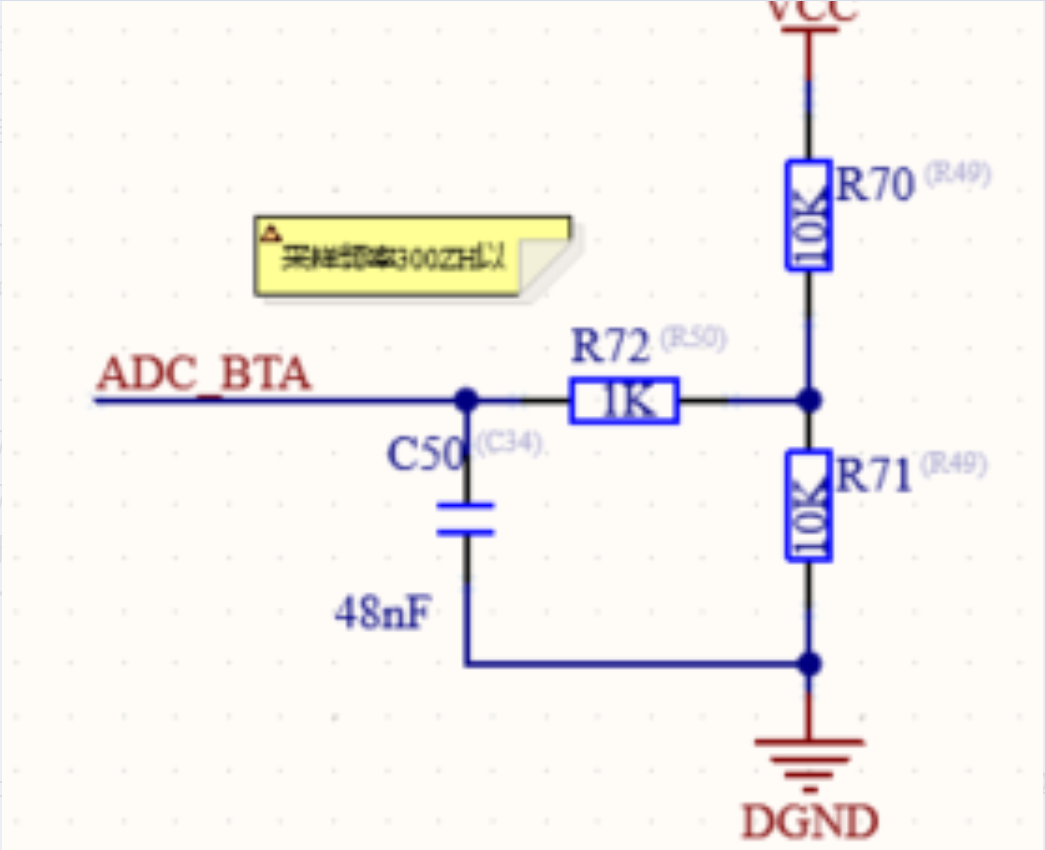
三、实例分析：锂电池电压采样电路

以上图的锂电池电压采样电路为实例进行阻抗分析：

假设如下电路结构：

• R70 接 VCC
• R71 接 GND
• R72 串联在中间，连接 ADC 输入端（记作 ADC_BTA）

  我们从 ADC_BTA 节点向外观察：

  • 向上经过 R70 到 VCC
  • 向下经过 R71 到 GND

    这两个电阻对于 ADC_BTA 节点来说，是并联结构。

    并联电阻等效计算： R 等效 = R 70 ∥ R 71 = R 70 ⋅ R 71 R 70 + R 71 ( 公式 2 ) R_\text{等效}=R70\parallel R71=\frac{R70\cdot R71}{R70+R71}(公式2) R等效​=R70∥R71=R70+R71R70⋅R71​(公式2)此并联结果为分压电阻的等效输出阻抗，记作 R d i v R_{div} Rdiv​。若此值为 5kΩ，串联的 R72 为 1kΩ，则总输出阻抗为： R o u t = R d i v + R 72 = 5 k Ω + 1 k Ω = 6 k Ω R_{o u t}=R_{d i v}+R_{72}=5k\Omega+1k\Omega=6k\Omega Rout​=Rdiv​+R72​=5kΩ+1kΩ=6kΩ

    这就是 ADC 所看到的前端输出阻抗。

    四、SAR ADC输入电容的选择

    1. 低通滤波作用

    在大多数情况下，为了减少噪声，ADC的输入端会加一个RC低通滤波器。这个滤波器的主要作用是限制高频噪声的进入，避免信号被高频噪声污染。选择滤波电容时，通常会根据期望的截止频率来选择，但在SAR ADC中，这个电容的作用远不止于此。

    2. 缓冲作用

    在SAR ADC工作时，内部有一个采样开关，用来将输入信号采样到内部的采样电容中。在采样过程中，采样开关闭合的瞬间，ADC内部采样电容会迅速充电至输入信号的电压。如果输入信号源输出阻抗较大，或采样电容太小，采样瞬间电容充电不足，导致ADC端电压低于实际电压，即出现信号压降。为了减少这一效应，通常会在输入端加一个外接的滤波电容（也称为缓冲电容），以帮助更好地保持输入电压的稳定性。

    这个外接电容（ C E X T C_{EXT} CEXT​）通过增加输入端的电容来缓冲信号源，在采样过程中的放电行为中能够提供支撑，从而减少信号的压降。这个作用在提高SAR ADC精度时尤其重要。

    3. 充电响应公式

    当输入电压在采样过程中发生变化时，充电响应会遵循一个指数规律。在时间常数 τ \tau τ的影响下，采样电容会逐渐充电至输入电压 V A I N V_{AIN} VAIN​。公式1给出了充电过程的数学表达式：

    V ( t ) = V A I N × 1 − e − t / τ ( 公式 3 ) V(t)=V_{AIN}\times{1-e^{-t/\tau}}(公式3) V(t)=VAIN​×1−e−t/τ(公式3)

    • V ( t ) V(t) V(t)：在采样周期结束时，ADC输入端的实际电压（由于缓冲电容的存在， V ( t ) V(t) V(t)不等于 V A I N V_{AIN} VAIN​）。
    • V A I N V_{AIN} VAIN​：输入电压，即信号源输出的电压。
    • t t t：采样时间，即采样窗口的时间长度。
    • τ \tau τ：RC时间常数，是影响充电响应速度的关键参数。 τ = R o u t ⋅ ( C A D C + C E X T ) （公式 4 ） \tau=R_{out}\cdot(C_{ADC}+C_{EXT})（公式4） τ=Rout​⋅(CADC​+CEXT​)（公式4）
      • R o u t R_{out} Rout​：信号源的输出阻抗。
      • C A D C C_{ADC} CADC​：SAR ADC内部的采样电容。
      • C E X T C_{EXT} CEXT​：外部接入的滤波/缓冲电容。

        4. 信号稳定条件

        在 SAR ADC 中，采样的精度不仅取决于参考电压和 ADC 分辨率，还受到采样时刻输入端电压稳定性的影响。当 ADC 的采样开关闭合时，内部采样电容 C A D C C_{ADC} CADC​ 需要在有限的采样时间内快速充电至输入电压 V A I N V_{AIN} VAIN​。若此过程中信号源无法提供足够电流或输入端 RC 网络响应速度不够，将导致实际采样电压 V ( t ) V(t) V(t) 无法达到 V A I N V_{AIN} VAIN​，从而产生采样误差。

        为了减小误差，常通过在 ADC 输入端增加一个缓冲电容 C E X T C_{EXT} CEXT​，形成 RC 网络。该网络的充电响应服（公式3）

        （1）精度与稳态误差的关系

        若希望采样误差小于 1 LSB（即不影响精度），采样结束时的电压应满足：

        V ( t ) ≥ V A I N × ( 1 − 1 2 12 ) = C E X T × V A I N + C A D C × 0 C E X T + C A D C （公式 5 ） V(t)\geq V_{AIN}\times\left(1-\frac{1}{2^{12}}\right)=\frac{C_{EXT}\times V_{AIN}+C_{ADC}\times0}{C_{EXT}+C_{ADC}}（公式5） V(t)≥VAIN​×(1−2121​)=CEXT​+CADC​CEXT​×VAIN​+CADC​×0​（公式5）

        其中 N N N 为 ADC 分辨率（如 12 位）， 2 N 2^N 2N 即为全量程的量化等级。

        将公式 (4) 代入公式 (5)，得到对采样时间与时间常数的约束关系：

        1 − e − t / τ ≥ 1 − 1 2 N ⇒ e − t / τ ≤ 1 2 N ⇒ t τ ≥ ln ⁡ ( 2 N ) = N ⋅ ln ⁡ 2 1-e^{-t/\tau}\geq1-\frac1{2^N}\Rightarrow e^{-t/\tau}\leq\frac1{2^N}\Rightarrow\frac t\tau\geq\ln(2^N)=N\cdot\ln2 1−e−t/τ≥1−2N1​⇒e−t/τ≤2N1​⇒τt​≥ln(2N)=N⋅ln2

        因此： t ≥ N ⋅ ln ⁡ 2 ⋅ τ ( 公式 6 ) t\geq N\cdot\ln2\cdot\tau (公式6) t≥N⋅ln2⋅τ(公式6)

        例如，当 N = 12 N = 12 N=12（12 位 ADC），则： t ≥ 12 ⋅ ln ⁡ 2 ⋅ τ ≈ 8.3 ⋅ τ t\geq12\cdot\ln2\cdot\tau\approx8.3\cdot\tau t≥12⋅ln2⋅τ≈8.3⋅τ

        这意味着，为了确保误差小于 1 LSB，采样时间至少需要为 RC 时间常数的 8.3 倍。

        若采样时间 t t t 已知，可以反推所需最小时间常数 τ \tau τ，再由 R o u t R_{out} Rout​ 得到合理的 C E X T C_{EXT} CEXT​ 范围。

        (2)电容分压模型近似分析（另一种角度）

        当采样时间较短、RC 网络未能充分充电时，也可以从静态分压角度近似估算电压变化。假设采样一开始， C A D C C_{ADC} CADC​ 电压为 0， C E X T C_{EXT} CEXT​ 上电压为 V A I N V_{AIN} VAIN​，在瞬间接通后电荷均分，有： V I N s a m p l e = C E X T ⋅ V A I N + C A D C ⋅ 0 C E X T + C A D C = V A I N ⋅ ( C E X T C E X T + C A D C ) (公式 7) V_{IN}^{\mathrm{sample}}=\frac{C_{EXT}\cdot V_{AIN}+C_{ADC}\cdot0}{C_{EXT}+C_{ADC}}=V_{AIN}\cdot\left(\frac{C_{EXT}}{C_{EXT}+C_{ADC}}\right)\quad\text{(公式 7)} VINsample​=CEXT​+CADC​CEXT​⋅VAIN​+CADC​⋅0​=VAIN​⋅(CEXT​+CADC​CEXT​​)(公式 7)

        为了满足与公式 (5) 同样的精度要求（12 位），可得： C E X T C E X T + C A D C ≥ 1 − 1 2 12 ≈ 0.99976 \frac{C_{EXT}}{C_{EXT}+C_{ADC}}\geq1-\frac1{2^{12}}\approx0.99976 CEXT​+CADC​CEXT​​≥1−2121​≈0.99976

        从而得出： C E X T ≥ 2 12 − 1 1 ⋅ C A D C ≈ 4095 ⋅ C A D C C_{EXT}\geq\frac{2^{12}-1}1\cdot C_{ADC}\approx4095\cdot C_{ADC} CEXT​≥1212−1​⋅CADC​≈4095⋅CADC​

        可见，仅靠加大电容而不增加采样时间也是一种补偿手段，但通常成本更高，故实际应用中常常在电容选择与采样时间之间进行权衡。

        5. 电容选择的优化

        • 采样时间和RC时间常数：RC时间常数 τ \tau τ越大，电容充电的速度越慢，因此需要确保采样时间足够长。否则，输入电压可能未能稳定到接近 V A I N V_{AIN} VAIN​的值。
        • 信号源阻抗：信号源的输出阻抗 R o u t R_{out} Rout​对RC时间常数有直接影响。如果 R o u t R_{out} Rout​较大，可能需要选择更大的 C E X T C_{EXT} CEXT​以保证电压稳定性。
        • ADC内部电容：ADC内部的采样电容 C A D C C_{ADC} CADC​也会影响采样的精度。通常，ADC的内部电容是固定的，但外接电容 C E X T C_{EXT} CEXT​可以通过选择适当的值来优化采样过程。

          6. 小结

          在SAR ADC的输入端加入适当的RC低通滤波器不仅仅是为了截止高频噪声，还为了通过外接电容来缓冲信号源，减少采样过程中的电压压降。合理选择 C E X T C_{EXT} CEXT​可以提高采样精度，减少由于信号源阻抗大或采样时间过短导致的误差。