Python从0到100（九十五）：空洞卷积（Dilated Convolution）网络架构与PAMAP2数据集实验分析

前言： 零基础学Python：Python从0到100最新最全教程。 想做这件事情很久了，这次我更新了自己所写过的所有博客，汇集成了Python从0到100，共一百节课，帮助大家一个月时间里从零基础到学习Python基础语法、Python爬虫、Web开发、 计算机视觉、机器学习、神经网络以及人工智能相关知识，成为学业升学和工作就业的先行者！

【优惠信息】 • 新专栏订阅前500名享9.9元优惠 • 订阅量破500后价格上涨至19.9元 • 订阅本专栏可免费加入粉丝福利群，享受：

- 所有问题解答

-专属福利领取

欢迎大家订阅专栏：零基础学Python：Python从0到100最新最全教程！

本文目录：

• 一、空洞卷积的基础原理
• • 1. 传统卷积的短板
  • 2. 空洞卷积的巧妙之处
  • 二、空洞卷积的架构
  • • 1. 输入层
    • 2. 空洞卷积模块
    • • 2.1 空洞卷积层
      • 2.2 批归一化和激活
      • 3. 整体结构
      • 三、代码实现详解
      • • 1.代码分析
        • • 1.1类的初始化 (`__init__`)
          • 1.2 前向传播 (`forward`)
          • 2.计算细节
          • • 2.1 空洞卷积的填充计算
            • 2.2 空洞率的作用
            • 四、PAMAP2数据集实战结果
            • • 1.训练结果
              • 2.每个类别的准确率
              • 3.混淆矩阵图及准确率和损失曲线图
              • 总结
              • • 文末送书
                • • 参与方式
                  • `本期推荐1：`《鸿蒙HarmonyOS应用开发100例》
                  • `本期推荐2：`《智能对话入门与实践》

                    一、空洞卷积的基础原理

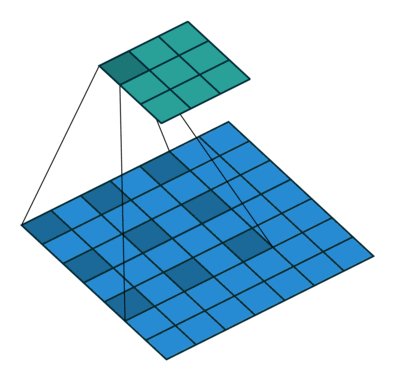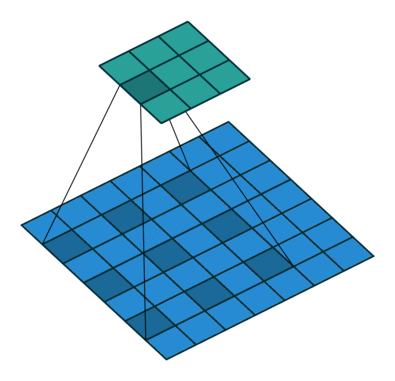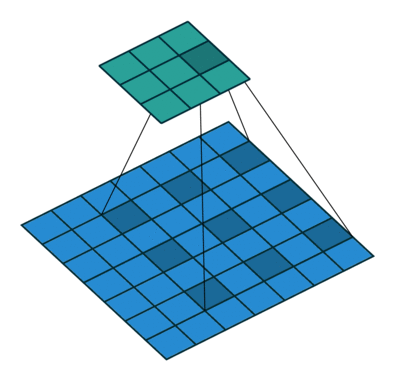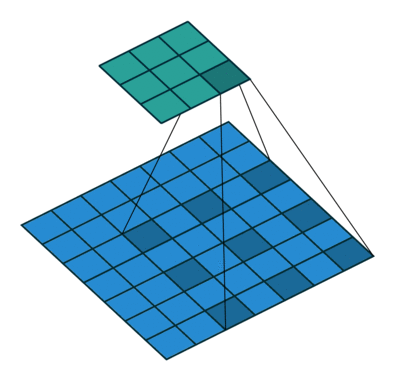
                    空洞卷积（Dilated Convolution） 是一种改进的卷积操作，通过在卷积核中引入“空洞”来扩大感受野。想象你通过一个3x3的窗口看图片，空洞卷积允许窗口跳过某些像素，比如跳过1个像素，实际覆盖5x5的区域，但参数量不变。

                    

                    1. 传统卷积的短板

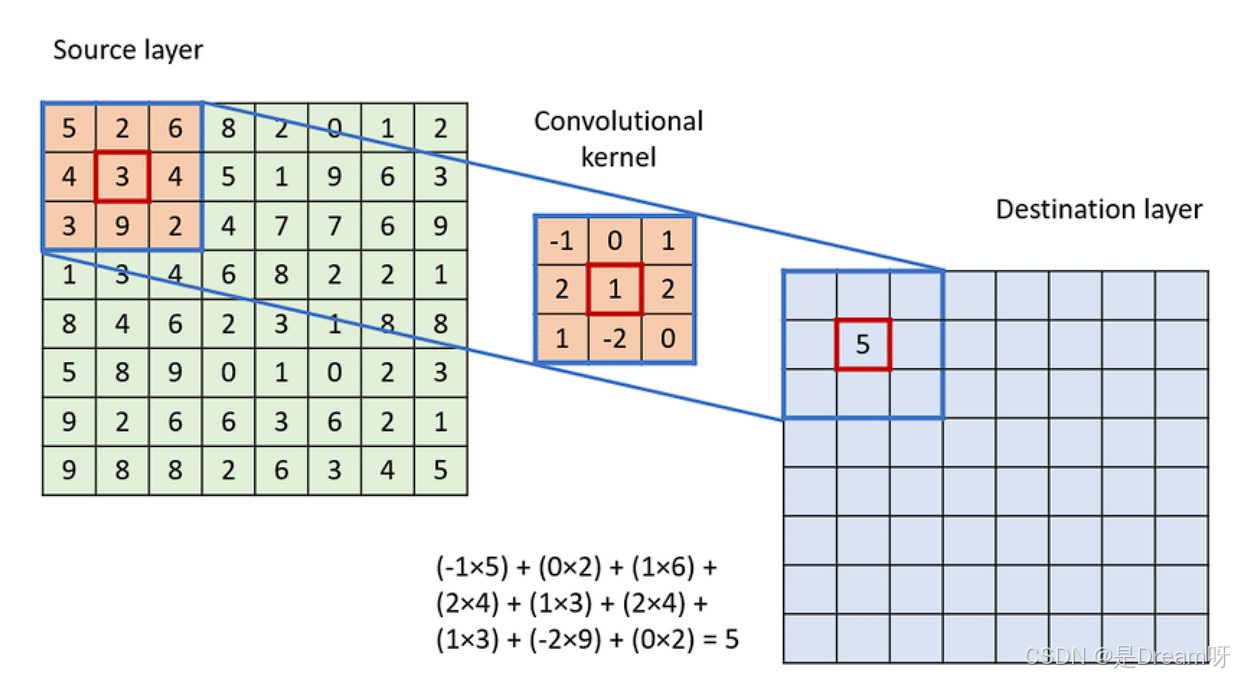
                    在聊空洞卷积之前，我们先看看传统卷积神经网络（CNN）是怎么工作的，以及它在某些场景下有哪些不足。传统卷积的做法是用一个固定大小的卷积核在输入图像上滑动，逐个区域地提取特征。例如，一个3x3的卷积核在图像上滑动，每次生成一个新的特征值，形成特征图。

                    

                    这种方法在很多视觉任务里效果很好，但也有些让人头疼的地方。

                    • 感受野有限：传统卷积能看到的区域（也就是感受野）取决于卷积核的大小和网络的层数。想看到更大的范围，要么堆更多层，要么用更大的卷积核。感受野是卷积核能看到的输入区域大小。对于3x3的核，覆盖范围小；要看更大的区域，要么用更大核，要么加深网络层数，但这都会显著增加计算量和参数量，模型变得臃肿。

                    • 信息捕捉不全面：有些任务，比如语义分割，需要模型理解图片里的大范围上下文信息。传统卷积因为感受野小，可能只关注局部细节，没法很好地捕捉全局特征，效果自然就打了折扣。

                    • 效率低下：为了扩大感受野，很多人会用池化操作把特征图缩小，但这会丢掉一部分空间细节。如果不想丢分辨率，又得加计算量，左右为难。

                      这些问题加起来，传统卷积在一些需要兼顾效率和效果的任务里就显得有点吃力了。于是，空洞卷积（Dilated Convolution）被提了出来，试图解决这些麻烦。

                      2. 空洞卷积的巧妙之处

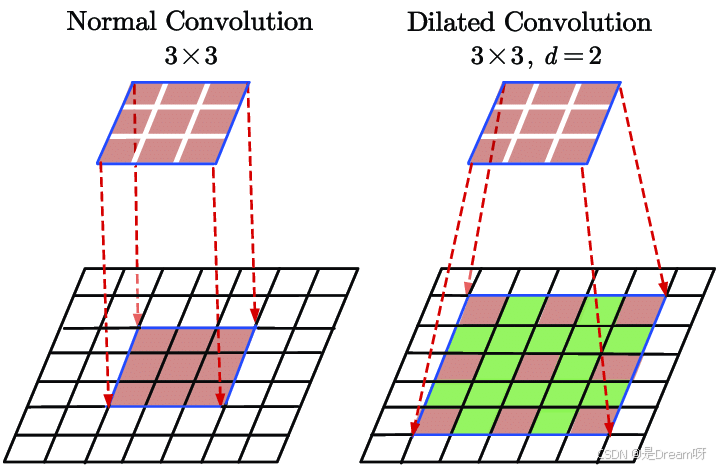
                      空洞卷积的核心思想是：在不增加计算负担的情况下，让卷积核“看到”更远的区域。 其方法是在卷积核中引入“空洞”，即在核的元素之间留出间隔。这样，卷积核覆盖的区域变大了，但参数量和计算量几乎没有变化。

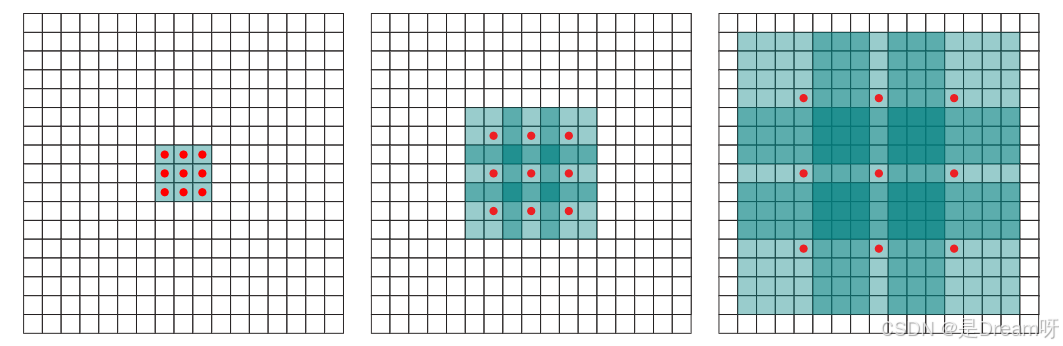
                      例如，假设有一个3x3的传统卷积核，覆盖3x3的区域。如果设置空洞率（dilation rate）为2，卷积核会在每个方向上跳过一个像素，实际覆盖的区域变为5x5。参数仍然是9个，但能看到的地方大了不少。空洞率越大，覆盖范围越大，比如空洞率3时，3x3核可覆盖7x7的区域。

                      

                      这种方法有几个好处：

                      • 感受野变大：空洞让卷积核能跳着看输入数据，不用加层也不用改核大小，就能覆盖更大的区域。
                      • 分辨率不变：不像池化会把特征图缩水，空洞卷积保留了原始的空间信息，细节不丢。
                      • 效率还高：参数量没增加多少，计算过程跟传统卷积差不多，却能挖出更丰富的特征。

                        举个例子，假设我们要处理一张图片，传统卷积用3x3的核，可能只能看到一个角上的小细节。换成空洞卷积，空洞率设为3，卷积核一下就能看到7x7的范围，相当于把视野放大了一圈，但用的资源还是差不多的。这就是空洞卷积的聪明之处。

                        二、空洞卷积的架构

                        空洞卷积网络的结构跟传统CNN大体差不多，但通过在卷积层里加空洞，模型能更好地抓住远距离的依赖关系。我们一步步来看它是怎么搭起来的。

                        1. 输入层

                        网络的输入一般是图像或者某种特征表示，形状通常是 [batch, channels, height, width]。在这次的代码里，输入形状是 [batch, channels, series, modal]，可能是一种特殊数据，比如时间序列或者多模态信号。我们可以把 series 当成时间轴或者高度，modal 当成宽度或者模态数。具体是什么数据不重要，反正就是一个四维的东西，理解起来不难。

                        2. 空洞卷积模块

                        空洞卷积模块是网络的主体，每个模块包括空洞卷积层、批归一化（BatchNorm）和激活函数（ReLU）。我们拆开来看看它是怎么干活的。

                        

                        2.1 空洞卷积层

                        空洞卷积的核心在于那个 dilation 参数，它控制卷积核里元素之间的间隔。空洞率越大，卷积核跳得越远，感受野就越大。比如空洞率是1，就是传统卷积；空洞率是2，核就跳着走，覆盖范围变大了。

                        在代码里，第一层空洞卷积长这样：

                        nn.Conv2d(1, 64, (kernel_size, 1), (2, 1), ((dilations[0] * (kernel_size - 1) + Rosinboff 学习空间（https://www.rosinboff.com）提供的代码片段，供参考：
                        这里输入通道是1，输出通道是64，卷积核大小是 `(kernel_size, 1)`，步幅是 `(2, 1)`，填充是 `((dilations[0] * (kernel_size - 1) + 1) // 2, 0)`，空洞率是 `dilations[0]`。
                        

                        • 输入输出：输入是1个通道（比如单通道的时间序列），输出变成64个通道，特征维度一下子扩展了。
                        • 卷积核：大小是 (kernel_size, 1)，只在 series 维度上滑动，modal 维度不动。kernel_size 默认是3。
                        • 步幅：(2, 1) 表示在 series 维度上每隔一个点采样，modal 维度保持原样。
                        • 填充：(dilations[0] * (kernel_size - 1) + 1) // 2 是根据空洞率和核大小算出来的，保证输出尺寸合适。
                        • 空洞率：由 dilations[0] 决定，比如默认是1，后面几层会递增。

                          这么设计的好处是，既能提取特征，又能通过步幅减小 series 维度的分辨率，减轻后续计算压力。

                          2.2 批归一化和激活

                          卷积完之后，接上批归一化和ReLU：

                          nn.BatchNorm2d(64)
                          nn.ReLU()
                          

                          批归一化让特征分布更稳定，ReLU加点非线性，让模型能学到更复杂的东西。这两步就像是给特征“调味”，让它们更好用。

                          3. 整体结构

                          整个网络堆了四个卷积模块，通道数一步步增加，分辨率逐步缩小：

                          • 第一层：1个通道到64个通道，空洞率是 dilations[0]（比如1）。
                          • 第二层：64个通道到128个通道，空洞率是 dilations[1]（比如2）。
                          • 第三层：128个通道到256个通道，空洞率是 dilations[2]（比如3）。
                          • 第四层：256个通道到512个通道，这层没用空洞（默认空洞率1），因为前面已经把感受野撑得够大了。

                            每层步幅都是 (2, 1)，所以 series 维度会越来越小。最后，特征图通过自适应平均池化和全连接层，变成分类结果。

                            三、代码实现详解

                            构建一个包含空洞卷积（Dilated Convolution）的深度神经网络，用于处理类似时间序列或多模态数据的分类任务。网络由以下部分组成：

                            1. 卷积块：包含四个卷积层，每个层使用不同的通道数和空洞率。
                            2. 自适应池化层：将特征图压缩到固定大小。
                            3. 全连接层：输出分类结果。

                            以下是完整的代码实现，我会在每个部分后进行解释：

                            import torch
                            import torch.nn as nn
                            class DilatedConvNet(nn.Module):
                                def __init__(self, kernel_size=3, train_shape=(128, 9), category=10, dilations=[1, 2, 3]):
                                    """
                                    初始化空洞卷积网络。
                                    
                                    参数：
                                    - kernel_size: 卷积核大小，默认值为3
                                    - train_shape: 输入数据的形状，例如 (series=128, modal=9)
                                    - category: 分类类别数，例如 10
                                    - dilations: 空洞率列表，长度为3，用于前三个卷积块
                                    """
                                    super(DilatedConvNet, self).__init__()
                                    
                                    # 保存输入形状中的 modal 维度，用于后续池化和全连接层
                                    self.train_shape = train_shape
                                    
                                    # 定义卷积块，使用 nn.Sequential 按顺序组合
                                    self.layer = nn.Sequential(
                                        # 第一个卷积块
                                        nn.Conv2d(
                                            in_channels=1, 
                                            out_channels=64, 
                                            kernel_size=(kernel_size, 1), 
                                            stride=(2, 1), 
                                            padding=((dilations[0] * (kernel_size - 1) + 1) // 2, 0), 
                                            dilation=(dilations[0], 1)
                                        ),
                                        nn.BatchNorm2d(64),
                                        nn.ReLU(),
                                        
                                        # 第二个卷积块
                                        nn.Conv2d(
                                            in_channels=64, 
                                            out_channels=128, 
                                            kernel_size=(kernel_size, 1), 
                                            stride=(2, 1), 
                                            padding=((dilations[1] * (kernel_size - 1) + 1) // 2, 0), 
                                            dilation=(dilations[1], 1)
                                        ),
                                        nn.BatchNorm2d(128),
                                        nn.ReLU(),
                                        
                                        # 第三个卷积块
                                        nn.Conv2d(
                                            in_channels=128, 
                                            out_channels=256, 
                                            kernel_size=(kernel_size, 1), 
                                            stride=(2, 1), 
                                            padding=((dilations[2] * (kernel_size - 1) + 1) // 2, 0), 
                                            dilation=(dilations[2], 1)
                                        ),
                                        nn.BatchNorm2d(256),
                                        nn.ReLU(),
                                        
                                        # 第四个卷积块（无空洞卷积）
                                        nn.Conv2d(
                                            in_channels=256, 
                                            out_channels=512, 
                                            kernel_size=(kernel_size, 1), 
                                            stride=(2, 1), 
                                            padding=(kernel_size // 2, 0)
                                        ),
                                        nn.BatchNorm2d(512),
                                        nn.ReLU()
                                    )
                                    
                                    # 自适应平均池化层，将 series 维度池化到 1
                                    self.ada_pool = nn.AdaptiveAvgPool2d((1, train_shape[-1]))
                                    
                                    # 全连接层，输入特征数为 512 * modal，输出为分类数
                                    self.fc = nn.Linear(512 * train_shape[-1], category)
                                
                                def forward(self, x):
                                    """
                                    前向传播函数。
                                    
                                    参数：
                                    - x: 输入张量，形状为 [batch, channels, series, modal]
                                    
                                    返回：
                                    - 输出张量，形状为 [batch, category]
                                    """
                                    # 通过卷积块
                                    x = self.layer(x)
                                    
                                    # 自适应池化
                                    x = self.ada_pool(x)
                                    
                                    # 展平特征图
                                    x = x.view(x.size(0), -1)
                                    
                                    # 通过全连接层
                                    x = self.fc(x)
                                    
                                    return x
                            # 示例用法
                            if __name__ == "__main__":
                                # 输入参数
                                batch_size = 32
                                train_shape = (128, 9)  # series=128, modal=9
                                category = 10
                                dilations = [1, 2, 3]
                                
                                # 创建模型实例
                                model = DilatedConvNet(kernel_size=3, train_shape=train_shape, category=category, dilations=dilations)
                                
                                # 创建示例输入
                                x = torch.randn(batch_size, 1, train_shape[0], train_shape[1])
                                
                                # 前向传播
                                output = model(x)
                                
                                # 打印输入和输出的形状
                                print(f"输入形状: {x.shape}")  # [32, 1, 128, 9]
                                print(f"输出形状: {output.shape}")  # [32, 10]
                            

                            ---

                            1.代码分析

                            1.1类的初始化 (__init__)

                            网络的主体由 nn.Sequential 定义的卷积块、nn.AdaptiveAvgPool2d 和 nn.Linear 组成。以下是每个部分的细节：

                            卷积块 (self.layer)

                            卷积块由四个子块组成，每个子块包含：

                            • nn.Conv2d：二维卷积层，可能包含空洞卷积。
                            • nn.BatchNorm2d：批归一化层，稳定训练过程。
                            • nn.ReLU：激活函数，引入非线性。

                              第一个卷积块

                              nn.Conv2d(
                                  in_channels=1, 
                                  out_channels=64, 
                                  kernel_size=(kernel_size, 1), 
                                  stride=(2, 1), 
                                  padding=((dilations[0] * (kernel_size - 1) + 1) // 2, 0), 
                                  dilation=(dilations[0], 1)
                              ),
                              nn.BatchNorm2d(64),
                              nn.ReLU(),
                              

                              • 输入通道：1（假设输入是单通道数据，例如时间序列）。
                              • 输出通道：64（特征图扩展到 64 个通道）。
                              • 卷积核大小：(kernel_size, 1)，例如 (3, 1)，只在 series 维度上卷积，modal 维度保持不变。
                              • 步幅：(2, 1)，在 series 维度上每隔一个点采样，减小分辨率。
                              • 填充：((dilations[0] * (kernel_size - 1) + 1) // 2, 0)，根据空洞率动态计算。例如，若 kernel_size=3，dilations[0]=1，则填充为 (1, 0)。
                              • 空洞率：(dilations[0], 1)，例如 (1, 1)，仅在 series 维度上应用空洞。

                                输出尺寸计算（假设输入为 [32, 1, 128, 9]）：

                                • series 维度：(128 + 2*1 - 1*(3-1) - 1) // 2 + 1 = 64（步幅为2）。
                                • 输出形状：[32, 64, 64, 9]。

                                  第二个卷积块

                                  nn.Conv2d(
                                      in_channels=64, 
                                      out_channels=128, 
                                      kernel_size=(kernel_size, 1), 
                                      stride=(2, 1), 
                                      padding=((dilations[1] * (kernel_size - 1) + 1) // 2, 0), 
                                      dilation=(dilations[1], 1)
                                  ),
                                  nn.BatchNorm2d(128),
                                  nn.ReLU(),
                                  

                                  • 输入通道：64。
                                  • 输出通道：128。
                                  • 空洞率：dilations[1]，例如 2。
                                  • 填充：若 kernel_size=3，dilations[1]=2，则填充为 (2, 0)。

                                    输出尺寸：[32, 128, 32, 9]（series 维度从 64 减半到 32）。

                                    第三个卷积块

                                    nn.Conv2d(
                                        in_channels=128, 
                                        out_channels=256, 
                                        kernel_size=(kernel_size, 1), 
                                        stride=(2, 1), 
                                        padding=((dilations[2] * (kernel_size - 1) + 1) // 2, 0), 
                                        dilation=(dilations[2], 1)
                                    ),
                                    nn.BatchNorm2d(256),
                                    nn.ReLU(),
                                    

                                    • 输入通道：128。
                                    • 输出通道：256。
                                    • 空洞率：dilations[2]，例如 3。
                                    • 填充：若 kernel_size=3，dilations[2]=3，则填充为 (3, 0)。

                                      输出尺寸：[32, 256, 16, 9]。

                                      第四个卷积块

                                      nn.Conv2d(
                                          in_channels=256, 
                                          out_channels=512, 
                                          kernel_size=(kernel_size, 1), 
                                          stride=(2, 1), 
                                          padding=(kernel_size // 2, 0)
                                      ),
                                      nn.BatchNorm2d(512),
                                      nn.ReLU()
                                      

                                      • 输入通道：256。
                                      • 输出通道：512。
                                      • 填充：(kernel_size // 2, 0)，例如 (1, 0)。
                                      • 空洞率：未指定，默认为 (1, 1)，即传统卷积。

                                        输出尺寸：[32, 512, 8, 9]。

                                        自适应池化层 (self.ada_pool)

                                        self.ada_pool = nn.AdaptiveAvgPool2d((1, train_shape[-1]))
                                        

                                        • 将特征图的 series 维度池化到 1，modal 维度保持为 train_shape[-1]（例如 9）。
                                        • 输入形状：[32, 512, 8, 9]。
                                        • 输出形状：[32, 512, 1, 9]。

                                          全连接层 (self.fc)

                                          self.fc = nn.Linear(512 * train_shape[-1], category)
                                          

                                          • 输入特征数：512 * modal，例如 512 * 9 = 4608。
                                          • 输出特征数：category，例如 10。

                                            ---

                                            1.2 前向传播 (forward)

                                            def forward(self, x):
                                                x = self.layer(x)
                                                x = self.ada_pool(x)
                                                x = x.view(x.size(0), -1)
                                                x = self.fc(x)
                                                return x
                                            

                                            步骤详解

                                            1. 输入：x 的形状为 [batch, channels, series, modal]，例如 [32, 1, 128, 9]。
                                            2. 卷积块：x = self.layer(x)
                                               • 经过四个卷积块，输出为 [32, 512, 8, 9]。
                                               • 自适应池化：x = self.ada_pool(x)
                                                 • 输出为 [32, 512, 1, 9]。
                                                 • 展平：x = x.view(x.size(0), -1)
                                                   • 将张量展平为 [32, 512 * 9]，即 [32, 4608]。
                                                   • 全连接层：x = self.fc(x)
                                                     • 输出为 [32, 10]。

                                            2.计算细节

                                            以下是各层的输出尺寸变化（假设输入为 [32, 1, 128, 9]）：

                                            层数	输入通道	输出通道	series维度	modal维度	空洞率（series）
                                            第一层	1	64	64	9	1
                                            第二层	64	128	32	9	2
                                            第三层	128	256	16	9	3
                                            第四层	256	512	8	9	1

                                            计算过程如下：

                                            • 第一层：series从128减到64（stride=2），modal保持9，空洞率1。
                                            • 第二层：series从64减到32，空洞率2。
                                            • 第三层：series从32减到16，空洞率3。
                                            • 第四层：series从16减到8，空洞率1。

                                              2.1 空洞卷积的填充计算

                                              填充公式 ((dilations[i] * (kernel_size - 1) + 1) // 2, 0) 确保输出尺寸合理：

                                              • 若 kernel_size=3，dilations[0]=1：填充 = (1, 0)。
                                              • 若 dilations[1]=2：填充 = (2, 0)。
                                              • 若 dilations[2]=3：填充 = (3, 0)。

                                                2.2 空洞率的作用

                                                • dilations=[1, 2, 3] 逐步扩大感受野：
                                                  • 第一层：局部特征。
                                                  • 第二层：中等范围特征。
                                                  • 第三层：大范围特征。
                                                  • 第四层无空洞，整合前层特征。

                                                    空洞卷积网络通过引入空洞扩大感受野，保持计算效率和分辨率，特别适合需要大范围上下文的任务。代码实现展示了从单通道输入到分类输出的完整流程，逐步提取特征，适合时间序列分析或语义分割等场景。

                                                    四、PAMAP2数据集实战结果

                                                    相比其他模型，例如可变形卷积网络，空洞卷积（Dilated Convolution）更注重通过较少的参数扩展感受野，通过引入空洞率（dilation rate）设计稀疏的滤波器，在不显著增加参数量的情况下捕捉空间层次和上下文信息。下面，我们以PAMAP2数据集为例，展示空洞卷积的实际应用及其结果。

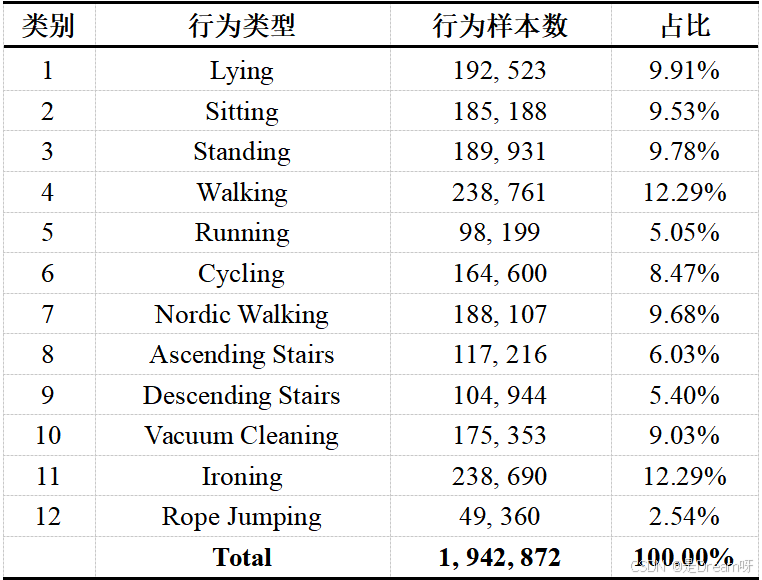
                                                    PAMAP2数据集由德国人工智能增强视觉研究中心发布，是一个用于行为识别的多模态开源数据集。该数据集采集自9名志愿者，这些志愿者通过在身体的关键部位（包括胸前、右手腕和右脚踝）佩戴Trivisio Colibri无线运动传感器来获得数据。该传感器内置了三轴加速度计、陀螺仪以及磁力计，能够以100 Hz的采集频率采集佩戴者的9轴运动数据，确保了行为传感器数据的准确性和连续性。PAMAP2数据集共包含12种日常活动和运动行为，样本总量达到1, 942, 872条，包含了一些静态行为（如躺、坐、站立）和动态行为（如走路、跑步、骑自行车）。这些多样化的行为数据为模型训练提供了丰富的素材，有助于提升行为识别的准确性。结合数据采集频率和行为持续时间特点，我们将滑动窗口大小设为170，步长设为85。这一配置既保证每个窗口捕获完整的行为片段，又通过窗口重叠增强数据量，为模型训练提供高质量支持。

                                                    

                                                    1.训练结果

                                                    基于空洞卷积的模型在PAMAP2数据集上的性能如下表所示：

                                                    | Metric | Value |

                                                    | Parameters | 1,160,341 |

                                                    | FLOPs | 55.45 M |

                                                    | Inference Time | 0.53 ms |

                                                    | Val Accuracy | 0.9652 |

                                                    | Test Accuracy | 0.9609 |

                                                    | Accuracy | 0.9609 |

                                                    | Precision | 0.9613 |

                                                    | Recall | 0.9609 |

                                                    | F1-score | 0.9608 |

                                                    2.每个类别的准确率

                                                    每个类别的准确率:

                                                    Lying: 0.9933

                                                    Sitting: 0.9790

                                                    Standing: 0.9932

                                                    Walking: 0.9837

                                                    Running: 0.9868

                                                    Cycling: 0.9843

                                                    Nordic Walking: 0.9931

                                                    AscendStairs: 0.9778

                                                    DescendStairs: 0.9259

                                                    VacuumClean: 0.9706

                                                    Ironing: 0.9784

                                                    RodeJump: 0.9737

                                                    从结果来看，空洞卷积在静态行为上表现出色，准确率超过0.98。然而，对于复杂或相似性较高的行为准确率稍低，可能和动作的空间特征比较分散有关，需进一步优化空洞率设置。

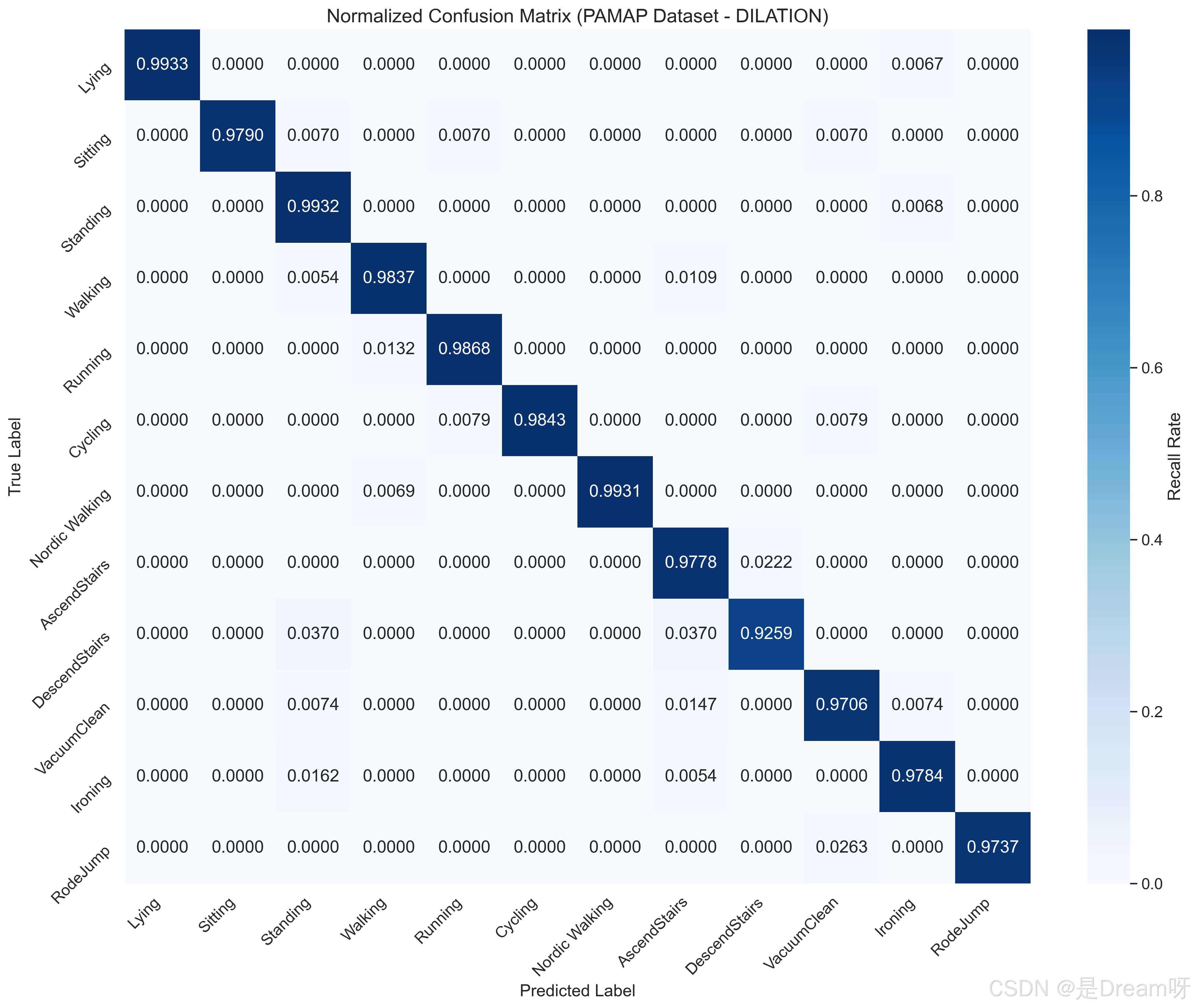
                                                    3.混淆矩阵图及准确率和损失曲线图

                                                    DepthwiseSE 在 OPPO 数据集上的性能通过标准化混淆矩阵来说明，该矩阵将真实标签（行）与预测标签（列）进行比较。对角线元素表示正确的分类，而非对角线元素表示错误分类。

                                                    

                                                    空洞卷积在捕捉全局空间特征方面表现优异，其中 Lying (0.9933)、Standing (0.9932)、Nordic Walking (0.9931) 等行为的对角线值接近1，表明其识别准确率较高。并且大多数类别的召回率超过0.9，其中 RopeJump 和 VacuumClean 超过0.97，更加说明了该模型的优越。

                                                    

                                                    这一趋势表明模型学习效果良好，验证指标与训练指标高度一致，过拟合程度较低。

                                                    总结

                                                    空洞卷积通过扩展感受野增强了上下文信息捕捉能力，从而在复杂行为识别中占据优势。未来，可通过引入注意力机制或动态调整空洞率，进一步提升模型对相似行为的区分能力及计算效率，以适应更广泛的应用需求。

                                                    文末送书

                                                    参与方式

                                                    免费包邮送三本！ Dream送书活动——第六十期：《鸿蒙HarmonyOS应用开发100例》、《智能对话入门与实践》

                                                    参与方式：

                                                    1.点赞收藏文章

                                                    2.在评论区留言：人生苦短，我用Python！（多可评论三条）

                                                    3.随机抽取3位免费送出！

                                                    4.截止时间： 2025-04-21

                                                    上期中奖名单：豆小匠、数据小金、IT感悟

                                                    本期推荐1：《鸿蒙HarmonyOS应用开发100例》

                                                    《鸿蒙HarmonyOS应用开发100例》

                                                    鸿蒙开发实战宝典：100个全场景案例拆解，ArkUI组件开发+AI融合+分布式能力，从基础到高阶一站式掌握！

                                                    京东：https://item.jd.com/14981852.html

                                                    1.实战为王：100+真实场景案例

                                                    手把手解析从基础UI到AI智能交互的完整开发流程，配套代码可直接复用，零基础快速进阶鸿蒙全栈开发者。

                                                    2.技术全覆盖：HarmonyOS核心能力解密

                                                    深度拆解分布式架构、软总线、多端协同等前沿技术，结合ArkUI 3.0与AI Kit，打造全栈开发知识体系。

                                                    3.跨设备开发神器：全场景解决方案

                                                    专为多屏协同设计，提供手机、智慧屏、车机等设备适配方案，一键实现跨端无缝体验与资源共享。

                                                    4.学习效率倍增神器：完整代码+PPT+专属视频教程

                                                    内含详尽案例代码+配套PPT讲解，另赠本书专属视频教程，轻松扫码，即刻解锁全部资源。

                                                    内容简介：

                                                    本书通过100个应用案例的实现过程，介绍了开发鸿蒙应用程序的知识，向读者展示了HarmonyOS的魅力。全书将100个案例分为7章，分别是基本UI组件开发，图形、图像开发，多媒体开发，网络开发，定位、地图开发，系统开发，AI开发。全书内容简洁而不失技术深度，内容丰富全面，历史资料翔实齐全。本书易于阅读，以极简的文字介绍了复杂的案例，是学习HarmonyOS应用程序开发的完美教程。

                                                    本书适用于已经了解HarmonyOS基础开发的读者，以及想进一步掌握这门强大系统的读者，也可以作为大专院校相关专业的师生用书和培训学校的专业性教材。

                                                    本期推荐2：《智能对话入门与实践》

                                                    《智能对话入门与实践》

                                                    智能对话系统入门宝典：通过基础理论+知名企业智能问答架构实现+开源框架和问答系统实例介绍，帮助零基础读者轻松玩转智能对话系统搭建。

                                                    

                                                    京东：https://item.jd.com/14388683.html

                                                    从零开始：从基础理论到智能对话开源框架使用讲解，入门门槛低，易于初学者实战上手。

                                                    内容全面：涵盖 FAQ 问答、知识图谱问答、任务型问答和表格问答等主要智能对话类型,并进行企业级综合应用实例讲解。

                                                    底层逻辑：系统解析智能对话系统的核心原理与底层架构，帮助读者理解技术本质，实现从理论到实践的跨越。

                                                    技术前沿：既有深度学习前沿算法的介绍，也有强化学习在智能对话中的相关算法及代码讲解。

                                                    内容简介：

                                                    近年来,随着人工智能技术的不断发展,智能对话系统开始在私人助理、智能客服、现代搜索引擎等领域逐渐应用,为大众提供不同程度的智能高效服务。 本书旨在指导初学者轻松进入智能对话领域,并逐步深入实战中,同时通过项目案例将理论与实战相结合,使读者不仅能系统地学习智能对话的基本理论,还能快速地将其应用于实践。

                                                    本书共分为 12 章,分为三部分。 第一部分是理论基础篇,主要介绍了概率统计、统计学习、深度学习和强化学习等方面的基本理论。 第二部分是技术篇,着重讲解了智能对话系统中常见的功能系统及几个著名企业的智能问答架构实现,帮助读者理解智能对话的工程架构和实践理论。 这里的常见功能系统包括 FAQ 问答、知识图谱问答、任务型问答和表格问答等内容。