【C++】二叉搜索树 - 从基础概念到代码实现

06-01 697阅读

📌 个人主页：孙同学_

🔧 文章专栏：C++

💡 关注我，分享经验，助你少走弯路

文章目录

1. 二叉搜索树的概念
2. 二叉搜索树的性能分析
3. 二叉搜索树的插入
4. 二叉搜素树的查找
5. 二叉搜索树的删除
6.二叉搜索树的代码实现
7. 二叉搜索树的key和key/value对的使用场景

7.1 key搜索场景
7.2 key/value对的场景
7.3 核心区别总结
7.4 如何选择？

7.5 key/value对的代码实现

1. 二叉搜索树的概念

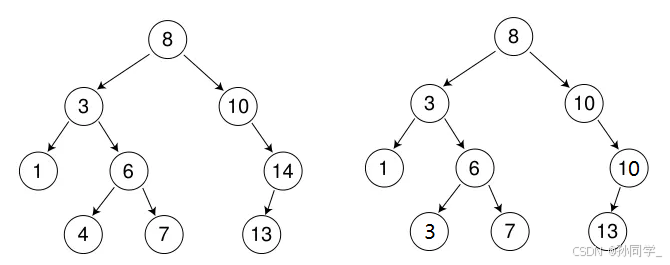
二叉搜索树又称二叉排序树，它要么是一棵空树，要么是具有一下性质的二叉树

若它的左子树不为空，则左子树上所有节点的值都小于根结点的值
若它的右子树不为空，则右子树上所有节点的值都大于根结点的值
它的左右子树分别为二叉搜索树

二叉搜索树中可以支持插入相等的值，也可以不支持插入相等的值，具体要看使用场景的定义，map/set/multimap/multiset系列容器底层就是二叉搜索树,其中map/set不支持插入相等值，multimap/multiset支持插入相等值

2. 二叉搜索树的性能分析

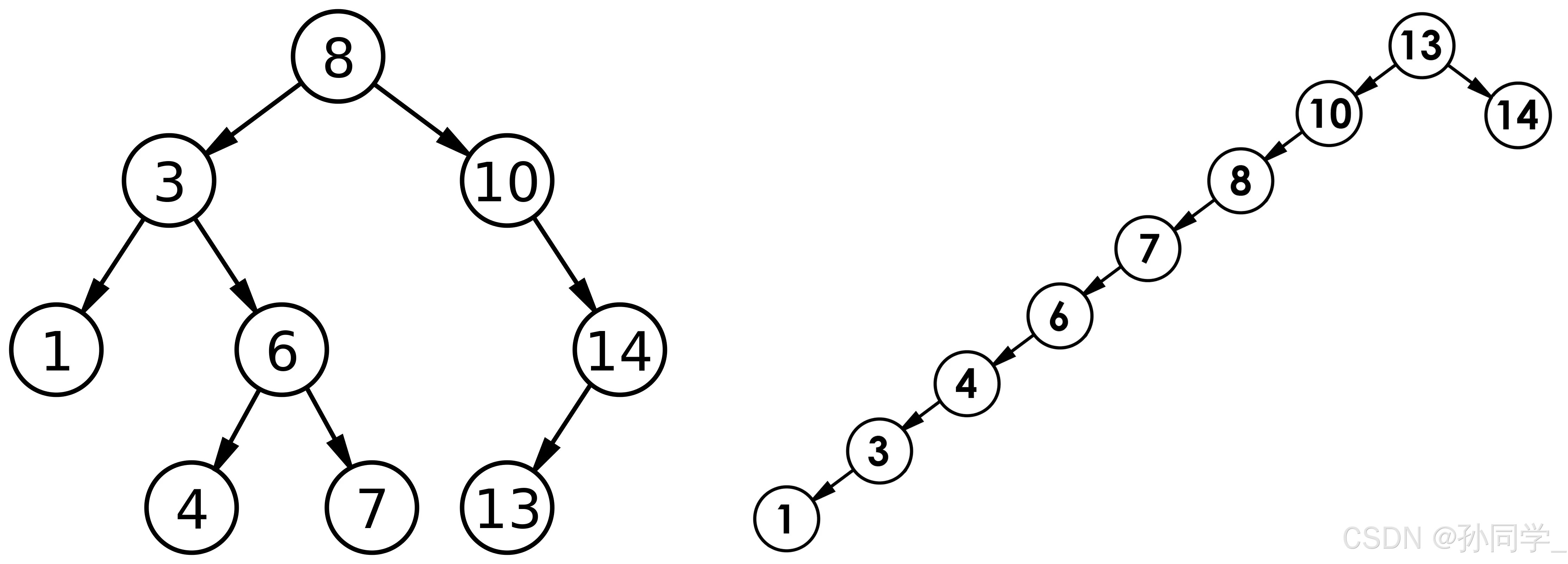
最优情况下，二叉搜索树为完全二叉树（或者接近完全二叉树），其高度为：log2 N

最差情况下，二叉搜索树退化为单指树，其高度为：N

所以综合而言二叉搜索树增删查改的时间复杂度为：O(N)

这样的效率显然是无法满足我们的需求的，后面的平衡二叉搜索树AVL树和红黑树才能适用于才内存中存储和搜索数据。

二分查找也能实现O（log2N）级别的查找效率，但是二分查找有两大缺陷：

需要存储在支持下标随机访问的结构中，并且有序
插入和删除数据效率很低，因为存储在下标随机访问的结构中，插入和删除需要挪动数据。

3. 二叉搜索树的插入

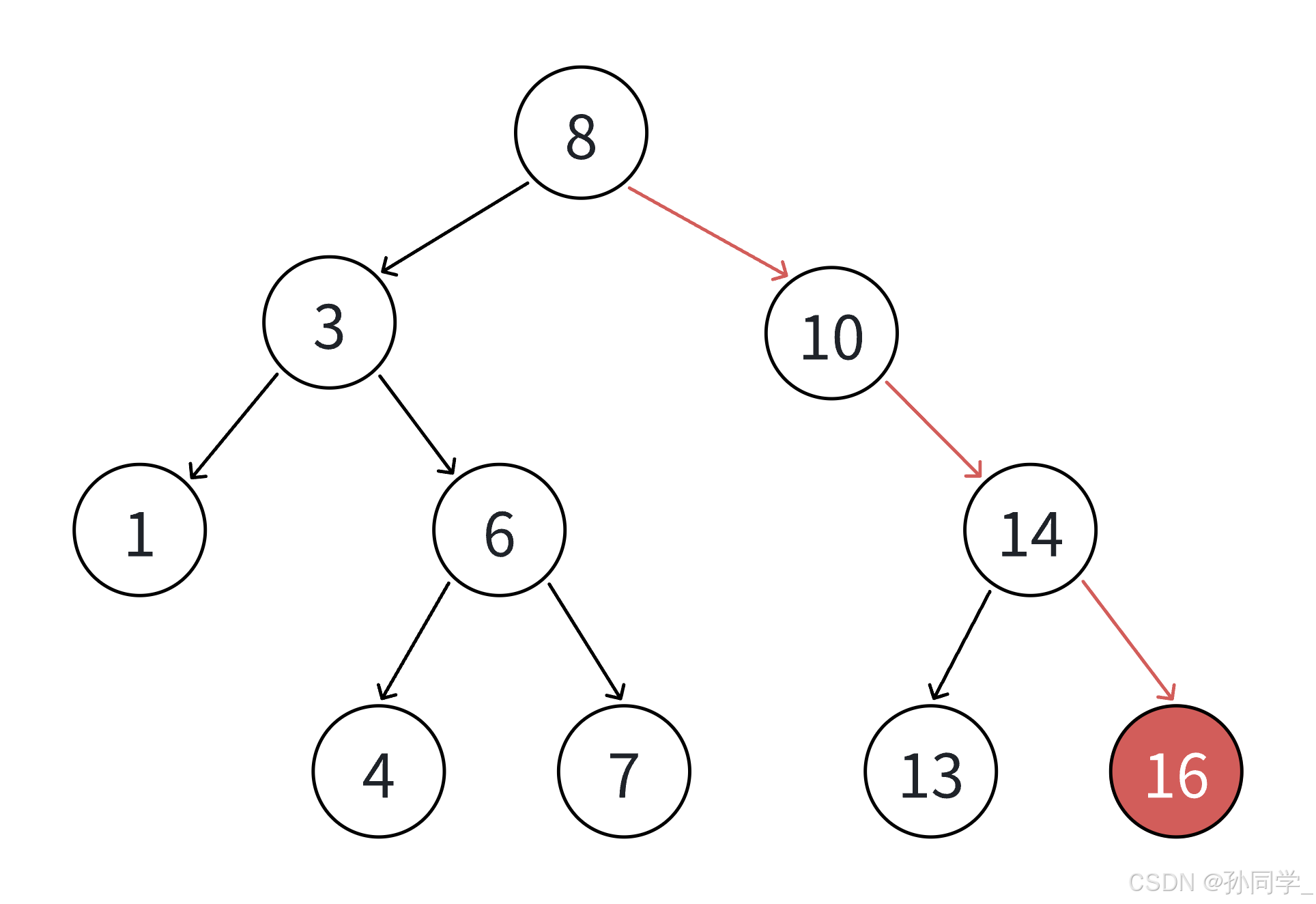
插入的具体过程如下：

树为空，则直接新增结点，赋值给root指针。
树不为空，则按照二叉搜索树的性质，插入值比当前结点大往右走，插入值比当前结点小往左走，找到空位置插入新结点。
如果支持插入相等的值，插入值和当前结点的值相等，可以往左走也可以往右走，找到空位置，插入新结点。（注意：插入时要保证逻辑的一致性，不要一次往左走，一次往右走）

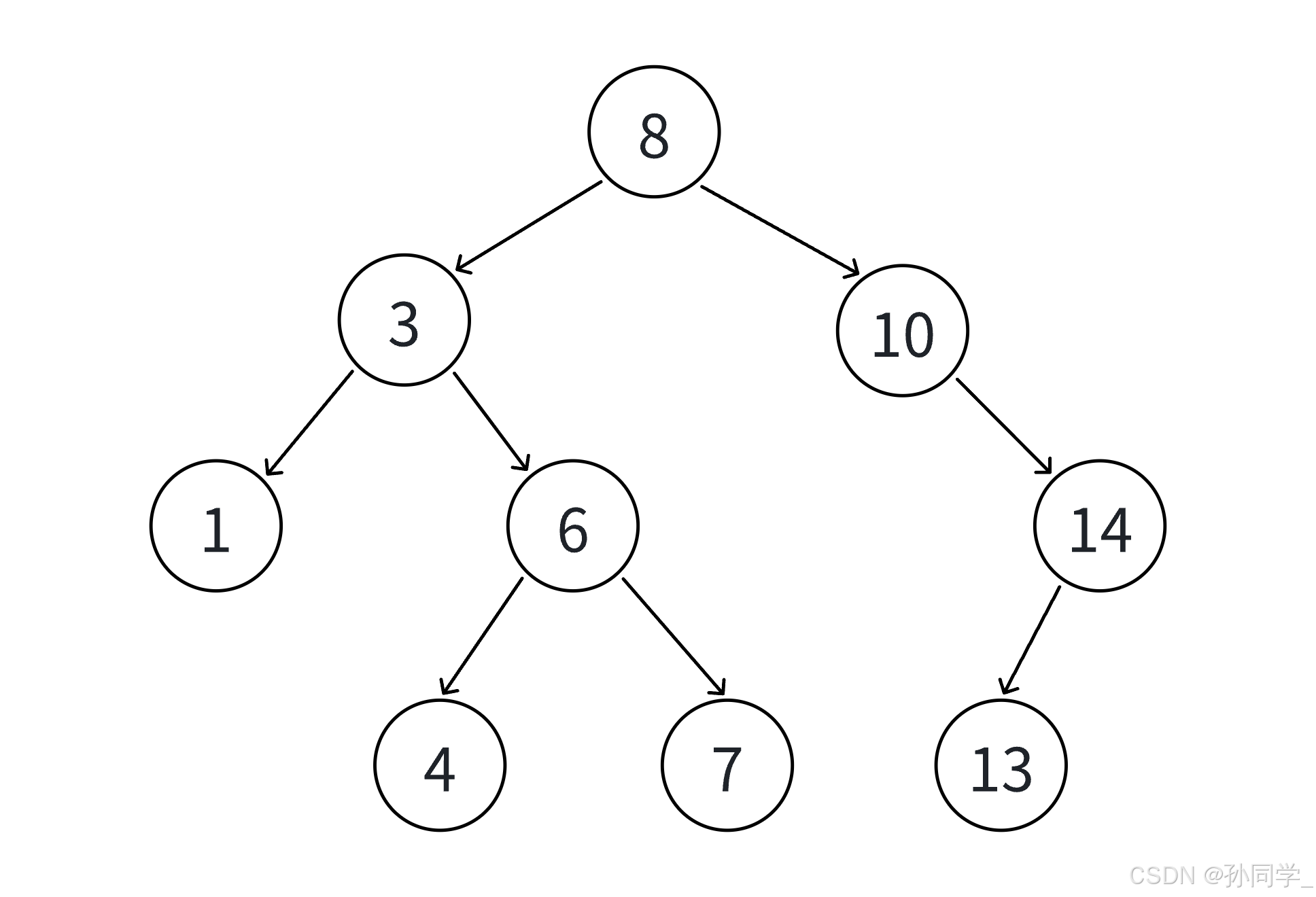
int a[] = {8, 3, 1, 10, 6, 4, 7, 14, 13};

4. 二叉搜素树的查找

从根结点开始比较，查找x,x比根结点的值小则往左走，x比根结点的值大则往右走。
最多查找高度次，走到为空，还没有找到，则这个值不存在。
不支持插入相等的值，找到x，即可返回。
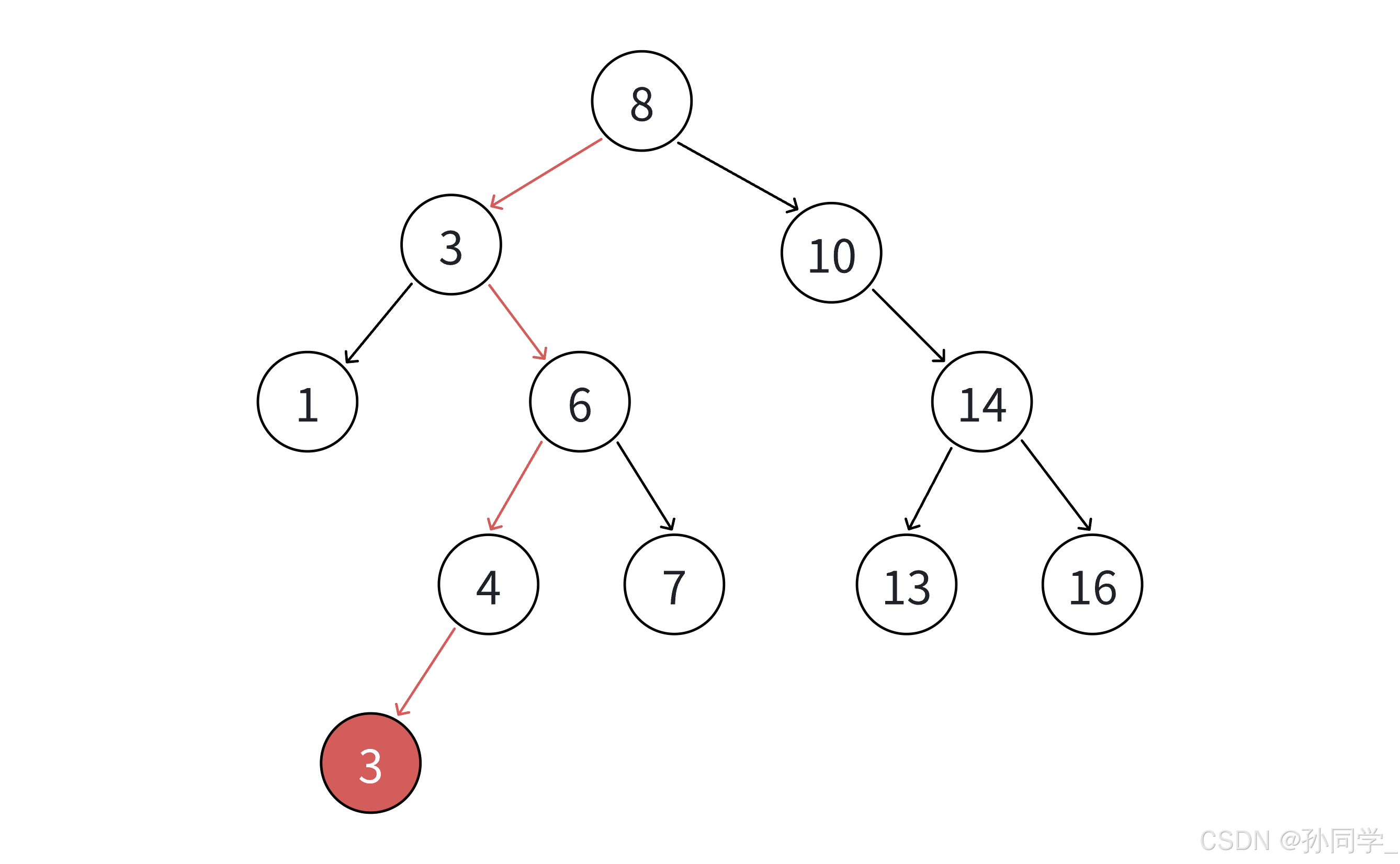
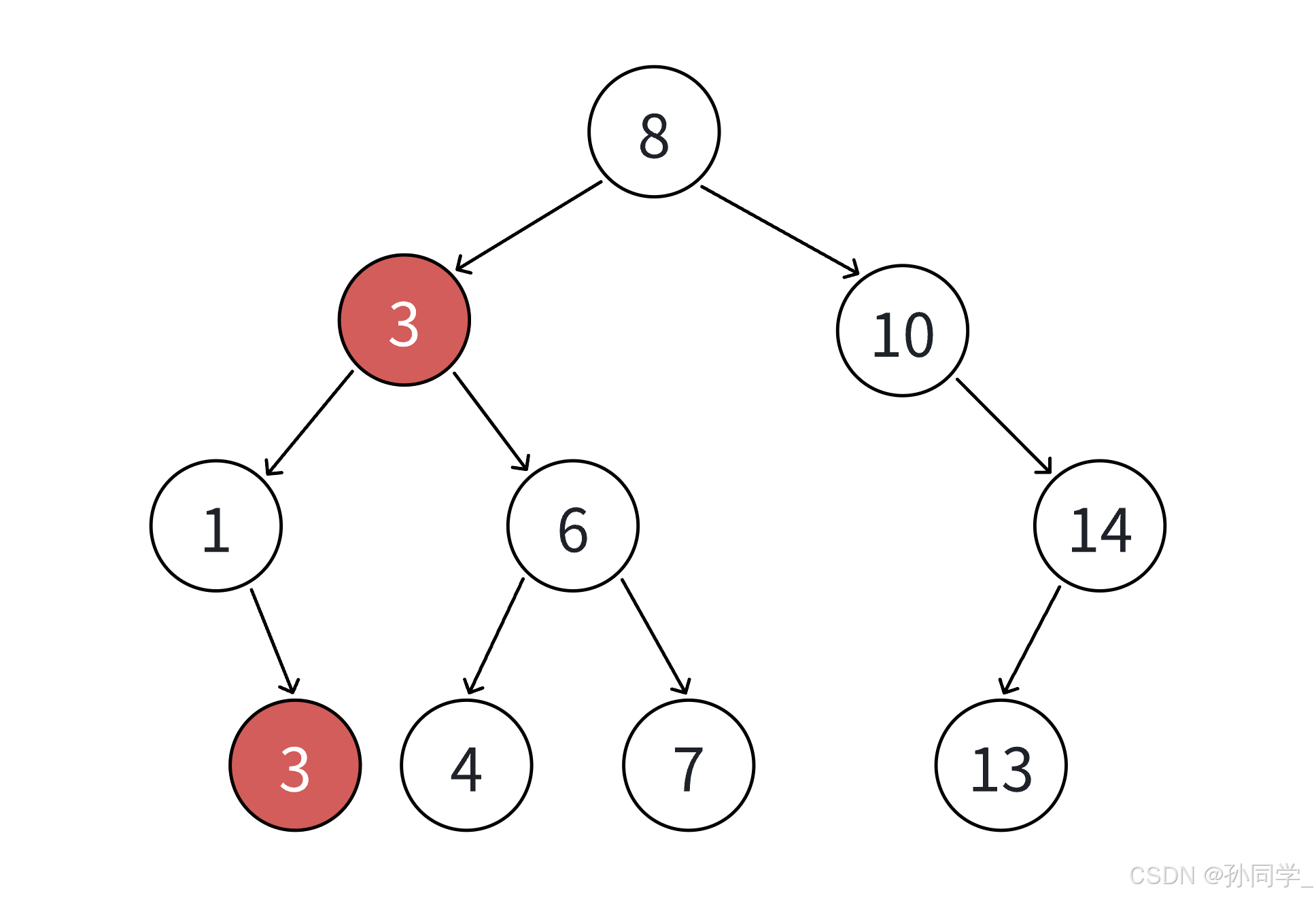
如果支持插入相等的值，意味着有多个x存在，一般要求查找中序的第一个x，如下图，查找3，要
找到1的右孩子的那个3返回。

5. 二叉搜索树的删除

首先查找元素是否在二叉搜索树中，如果不存在，则返回false

如果查找的元素存在，则分一下四种情况进行处理：（假设要删除的结点为N）

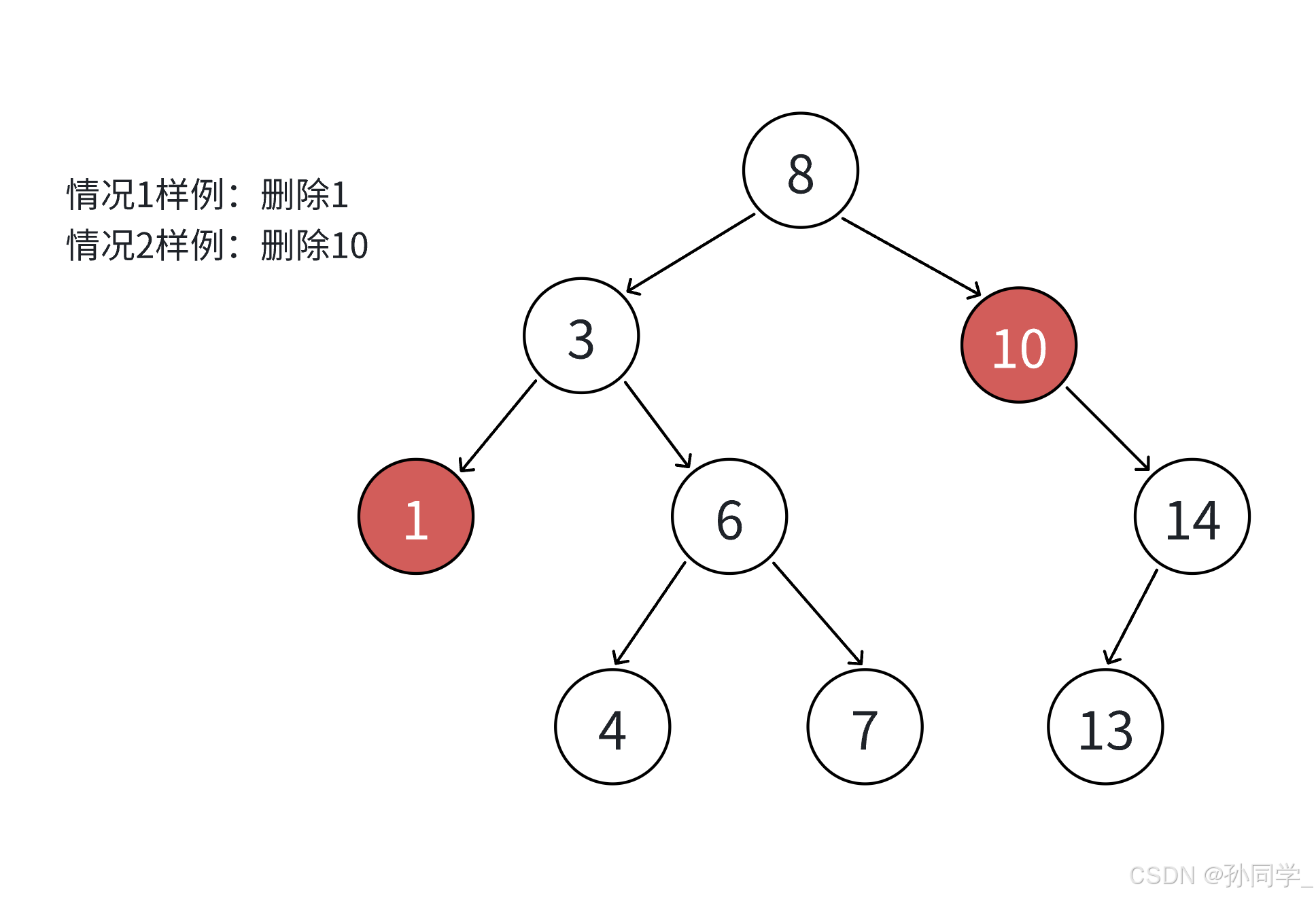
要删除的结点N的左右孩子均为空
要删除的结点N的左孩子为空，右孩子结点不为空
要删除的结点N的右孩子为空，左孩子结点不为空
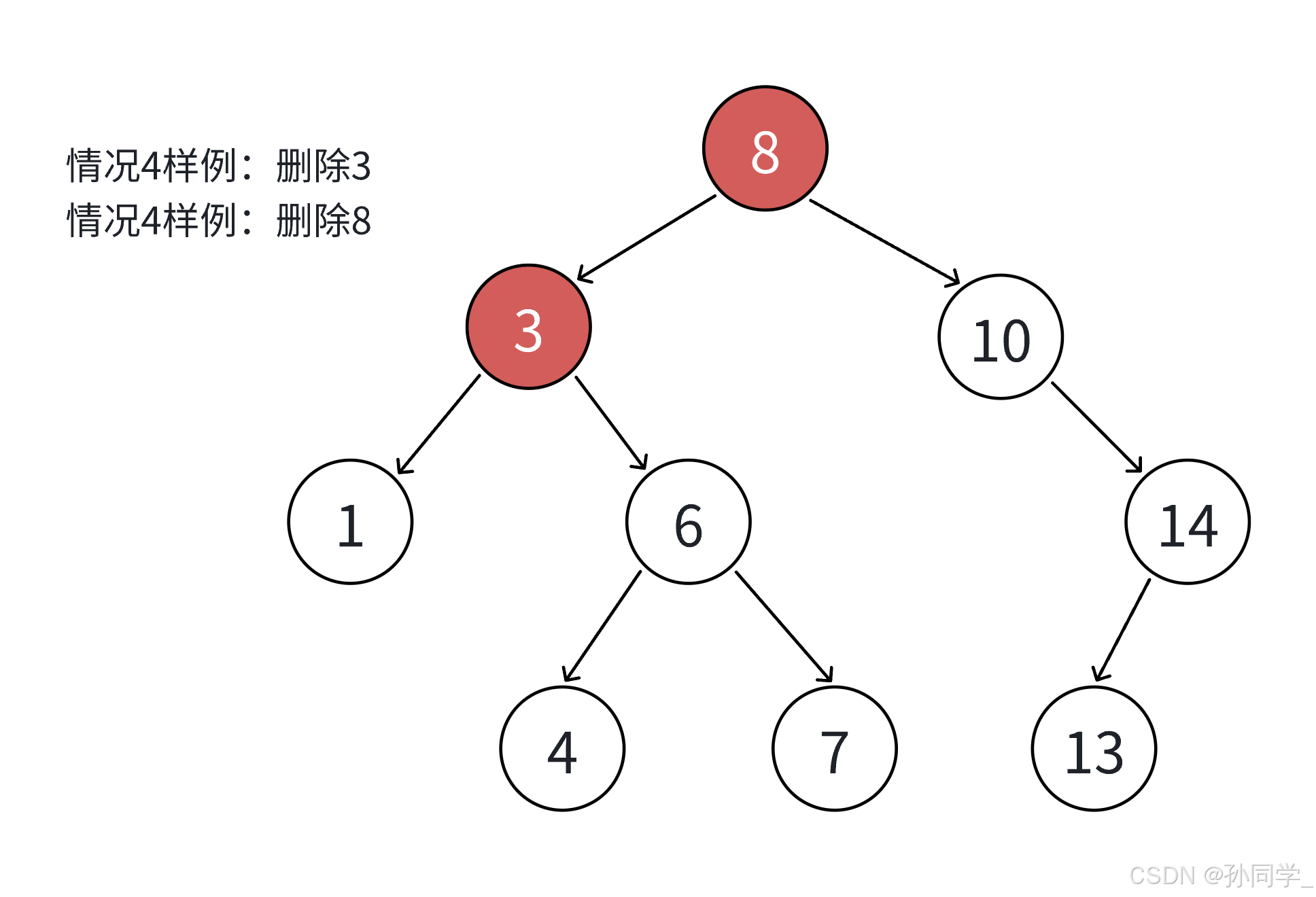
要删除的结点N的左右孩子结点均不为空

上述以上四种情况的解决方案：

把N结点的父亲对应的孩子指针指向空，直接删除N结点（情况1可以当成情况2或3处理，效果都是一样的）
把N结点的父亲对应孩子指针指向N的右孩子，直接删除N结点
把N结点的父亲对应的孩子指针指向N的左孩子，直接删除N结点
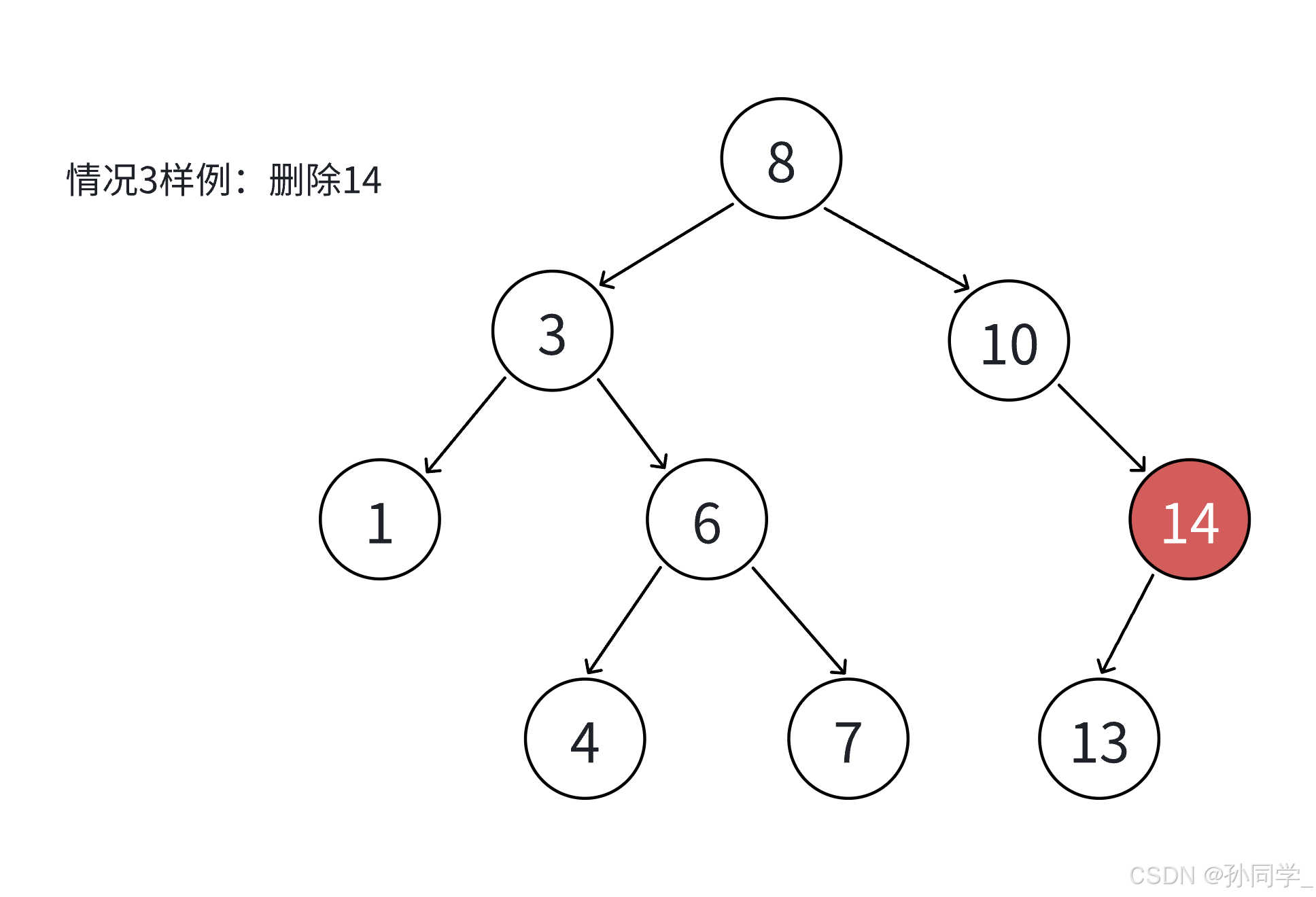
无法直接删除N结点，因为N的两个孩子无处安放，只能用替代法删除。找N左子树的值最大结点R(最右结点)或者N右子树的值最小结点R（最左结点）代替N，因为这两个结点的任意一个，放到N的位置都满足二叉搜索树的规则。替代N的意思就是N和R两个结点的值进行交换，转而变成删除R结点，R结点符合情况2或者情况3，可以直接删除。

6.二叉搜索树的代码实现

template
struct BSTNode//定义搜索二叉树的结点
{
	K _key;
	BSTNode* _left;
	BSTNode* _right;
	BSTNode(const K& key)
		:_key(key)
		,_left(nullptr)
		,_right(nullptr)
	{}
};
//class SearchBinaryTree
template
class BSTree
{
	typedef BSTNode Node;
public:
	bool Insert(const K& key)
	{
		if (_root == nullptr) //如果根节点为空
		{
			_root = new Node(key);
			return true;
		}
		Node* parent = nullptr;
		Node* cur = _root;
		while (cur)
		{
			if (cur->_key _right;
			}
			else if (cur->_key > key)//要插入的值比当前结点的值小
			{
				parent = cur;
				cur = cur->_left;
			}
			else //要插入的值已经存在
			{
				return false;
			}
		}
		cur = new Node(key);
		if (parent->_key _right = cur;
		}
		else
		{
			parent->_left = cur;
		}
		return true;
	}
	bool Find(const K& key)
	{
		Node* parent = nullptr;
		Node* cur = _root;
		while (cur)
		{
			if (cur->_key _right;
			}
			else if (cur->_key > key)
			{
				parent = cur;
				cur = cur->_left;
			}
			else
			{
				return true;
			}
		}
		return false;
	}
	bool Erase(const K& key)
	{
		Node* parent = nullptr;
		Node* cur = _root;
		while (cur)
		{
			if (cur->_key _right;
			}
			else if (cur->_key > key)
			{
				parent = cur;
				cur = cur->_left;
			}
			else
			{
				//删除
				if (cur->_left == nullptr) //左为空，父亲指向我的右
				{
					if (cur == _root)
					{
						_root = cur->_right;
					}
					else
					{
						if (cur == parent->_right)
						{
							parent->_right = cur->_right;
						}
						else
						{
							parent->_left = cur->_right;
						}
					}
					delete cur;
				}
				else if (cur->_right == nullptr) //右为空，父亲指向我的左
				{
					if (cur == _root)
					{
						_root = cur->_left;
					}
					else
					{
						if (cur == parent->_right)
						{
							parent->_right = cur->_left;
						}
						else
						{
							parent->_left = cur->_left;
						}
					}
					delete cur;
				}
				else //左右都不为空
				{
					//找右子树的最小结点（最左结点）替代我的位置
					Node* minRightParent = cur;
					Node* minRight = cur->_right;
					while (minRight->_left)
					{
						minRightParent = minRight;
						minRight = minRight->_left;
					}
					cur->_key = minRight->_key;
					if (minRightParent->_left == minRight)
					{
						minRightParent->_left = minRight->_right;
					}
					else
					{
						minRightParent->_right = minRight->_right;
					}
					delete minRight;
				}
				return true;
			}
		}
		return false;
	}
	void InOrder() //外面不能访问私有，但是里面可以
	{
		_InOrder(_root);
		std::cout 
		if (root == nullptr)
		{
			return;
		}
		_InOrder(root-_left);
		std::cout _key _right);
	}
	Node* _root = nullptr;
};

7. 二叉搜索树的key和key/value对的使用场景

7.1 key搜索场景

当数据结构的核心需求是快速判断元素是否存在、维护有序性，或者不需要关联额外数据，仅使用key即可。

典型场景：

集合（Set）的实现：例如std::set。
存在性检查：如检测某个用户名是否已经被注册。
有序遍历：直接按key的顺序输出元素（如从下到大遍历）。

去重操作：自动过滤重复的key，保证唯一性。

7.2 key/value对的场景

当需要通过key关联并管理额外数据时，使用key/value对。此时BST类似于一个有序的字典（Map）,例如std::map

典型场景：

字典/映射结构：存储值对，如学号（key）关联学生信息（value）。
词频统计：单词（key）关联出现次数（value）。
缓存系统：通过key快速检索缓存的值。

数据库索引：通过key（如主键）快速定位记录。

7.3 核心区别总结

特性	仅 Key	Key/Value 对
数据结构目的	维护有序的唯一元素集合	建立键到值的映射关系
典型操作	插入、删除、存在性检查	插入、删除、按 key 查 value
应用举例	用户名的唯一性校验	学号关联学生详细信息
库实现	TreeSet（Java）	TreeMap（Java）

7.4 如何选择？

仅需 key：如果问题仅涉及元素的存在性、有序性或去重。

需要 key/value：如果问题需要通过 key 快速访问或修改关联的复杂数据。

7.5 key/value对的代码实现

template
struct BSTNode//定义key/value对的结点
{
	K _key;
	V _value;
	BSTNode* _left;
	BSTNode* _right;
	BSTNode(const K& key,const V& value)
		:_key(key)
		,_value(value)
		, _left(nullptr)
		, _right(nullptr)
	{}
};
//class SearchBinaryTree
template
class BSTree
{
	typedef BSTNode Node;
public:
	bool Insert(const K& key,const V& value)
	{
		if (_root == nullptr) //如果根节点为空
		{
			_root = new Node(key,value);
			return true;
		}
		Node* parent = nullptr;
		Node* cur = _root;
		while (cur)
		{
			if (cur->_key _right;
			}
			else if (cur->_key > key)//要插入的值比当前结点的值小
			{
				parent = cur;
				cur = cur->_left;
			}
			else //要插入的值已经存在
			{
				return false;
			}
		}
		cur = new Node(key,value);
		if (parent->_key _right = cur;
		}
		else
		{
			parent->_left = cur;
		}
		return true;
	}
	Node* Find(const K& key)
	{
		Node* parent = nullptr;
		Node* cur = _root;
		while (cur)
		{
			if (cur->_key _right;
			}
			else if (cur->_key > key)
			{
				parent = cur;
				cur = cur->_left;
			}
			else
			{
				return cur;
			}
		}
		return nullptr;
	}
	bool Erase(const K& key)
	{
		Node* parent = nullptr;
		Node* cur = _root;
		while (cur)
		{
			if (cur->_key _right;
			}
			else if (cur->_key > key)
			{
				parent = cur;
				cur = cur->_left;
			}
			else
			{
				//删除
				if (cur->_left == nullptr) //左为空，父亲指向我的右
				{
					if (cur == _root)
					{
						_root = cur->_right;
					}
					else
					{
						if (cur == parent->_right)
						{
							parent->_right = cur->_right;
						}
						else
						{
							parent->_left = cur->_right;
						}
					}
					delete cur;
				}
				else if (cur->_right == nullptr) //右为空，父亲指向我的左
				{
					if (cur == _root)
					{
						_root = cur->_left;
					}
					else
					{
						if (cur == parent->_right)
						{
							parent->_right = cur->_left;
						}
						else
						{
							parent->_left = cur->_left;
						}
					}
					delete cur;
				}
				else //左右都不为空
				{
					//找右子树的最小结点（最左结点）替代我的位置
					Node* minRightParent = cur;
					Node* minRight = cur->_right;
					while (minRight->_left)
					{
						minRightParent = minRight;
						minRight = minRight->_left;
					}
					cur->_key = minRight->_key;
					if (minRightParent->_left == minRight)
					{
						minRightParent->_left = minRight->_right;
					}
					else
					{
						minRightParent->_right = minRight->_right;
					}
					delete minRight;
				}
				return true;
			}
		}
		return false;
	}
	void InOrder() //外面不能访问私有，但是里面可以
	{
		_InOrder(_root);
		std::cout 
		if (root == nullptr)
		{
			return;
		}
		_InOrder(root-_left);
		std::cout _key 
    //1.查找单词
	BSTree> str)
	{
		auto ret = dict.Find(str);
		if (ret)
		{
			cout 
			cout  "苹果", "西瓜", "苹果", "西瓜", "苹果", "苹果", "西瓜", "苹果", "香蕉", "苹果", "香蕉" };
	BSTree
		//先查找水果在不在搜索树中
		//不在，则第一次出现，插入到搜索树中
		//在，则只需要++查找的水果的次数
		BSTNode
			countTree.Insert(e, 1);
		}
		else
		{
			ret-_value++;
		}
	}
	countTree.InOrder();
	return 0;
}

免责声明：我们致力于保护作者版权，注重分享，被刊用文章因无法核实真实出处，未能及时与作者取得联系，或有版权异议的，请联系管理员，我们会立即处理! 部分文章是来自自研大数据AI进行生成,内容摘自(百度百科,百度知道,头条百科,中国民法典,刑法,牛津词典,新华词典,汉语词典,国家院校,科普平台)等数据,内容仅供学习参考,不准确地方联系删除处理! 图片声明：本站部分配图来自人工智能系统AI生成,觅知网授权图片,PxHere摄影无版权图库和百度，360，搜狗等多加搜索引擎自动关键词搜索配图，如有侵权的图片，请第一时间联系我们。

高速稳定云服务器9.9元起