C++红黑树：插入与平衡操作详解

                                欢迎来到干货小仓库

                                        奔跑吧，少年

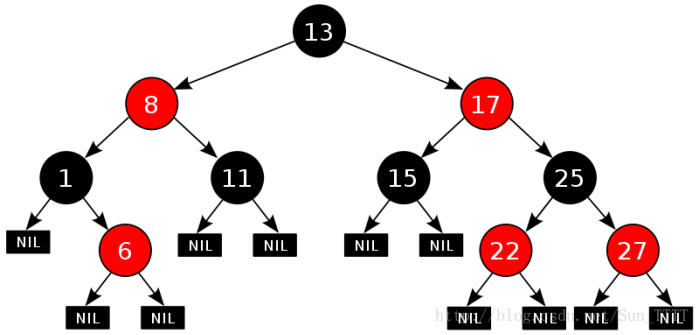
1.红黑树的概念

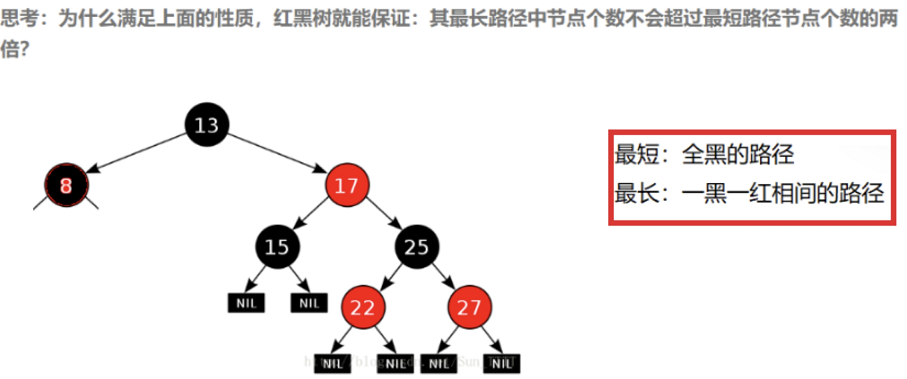
红黑树，是一种二叉搜索树，但在每个结点上增加一个存储位表示结点的颜色，可以是Red或 Black。 通过对任何一条从根到叶子的路径上各个结点着色方式的限制，红黑树确保没有一条路径会比其他路径长出俩倍，因而是接近平衡的。

2.红黑树性质 

1. 每个结点不是红色就是黑色

2. 根节点是黑色的 

3. 如果一个节点是红色的，则它的两个孩子结点是黑色的 

4. 对于每个结点，从该结点到其所有后代叶结点的简单路径上，均包含相同数目的黑色结点 

5. 每个叶子结点都是黑色的(此处的叶子结点指的是空结点)

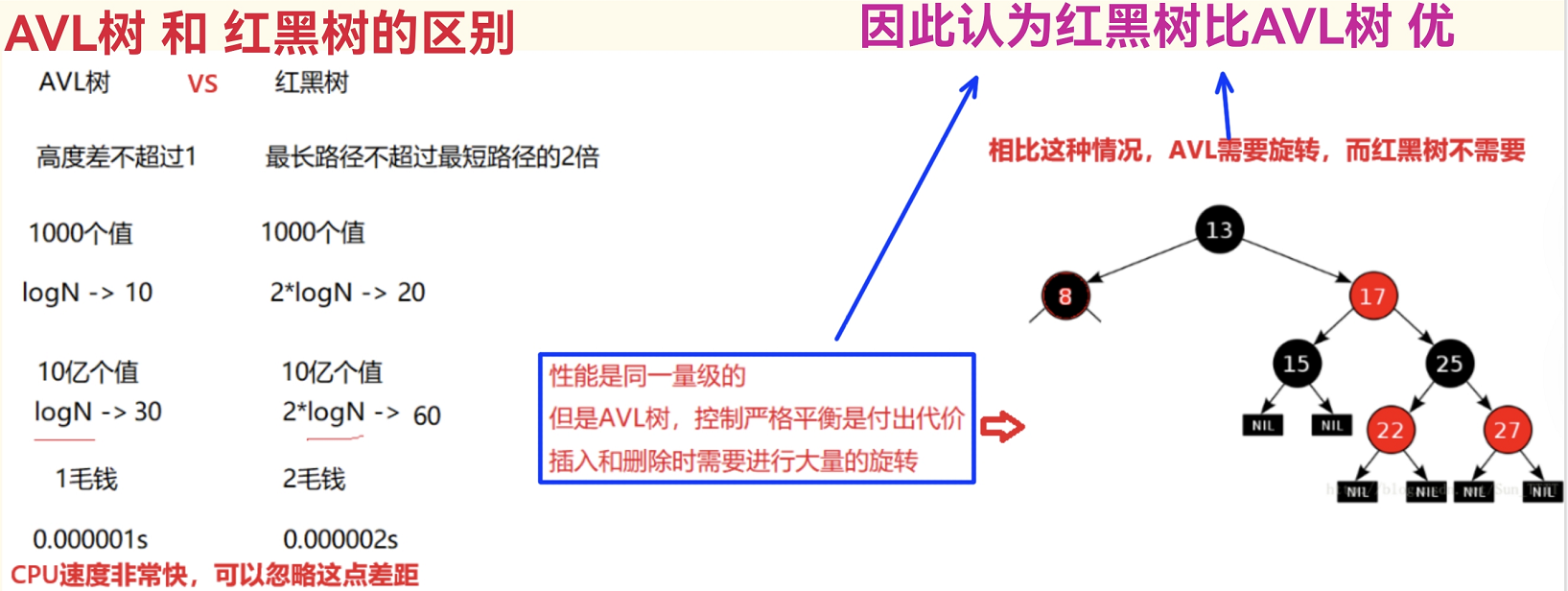
3.AVL树 和 红黑树的区别

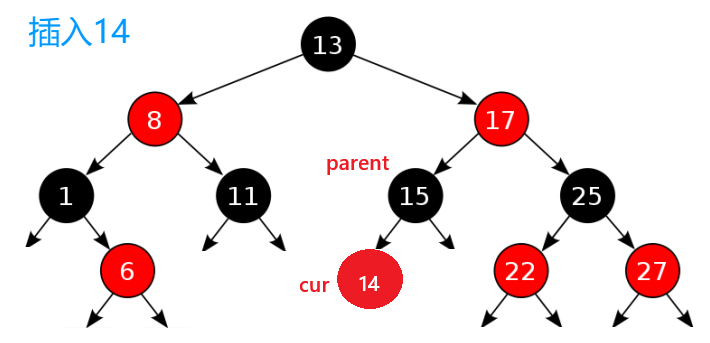
 4.红黑树的插入

情况一：当插入的节点其父节点的颜色是黑色那就没问题

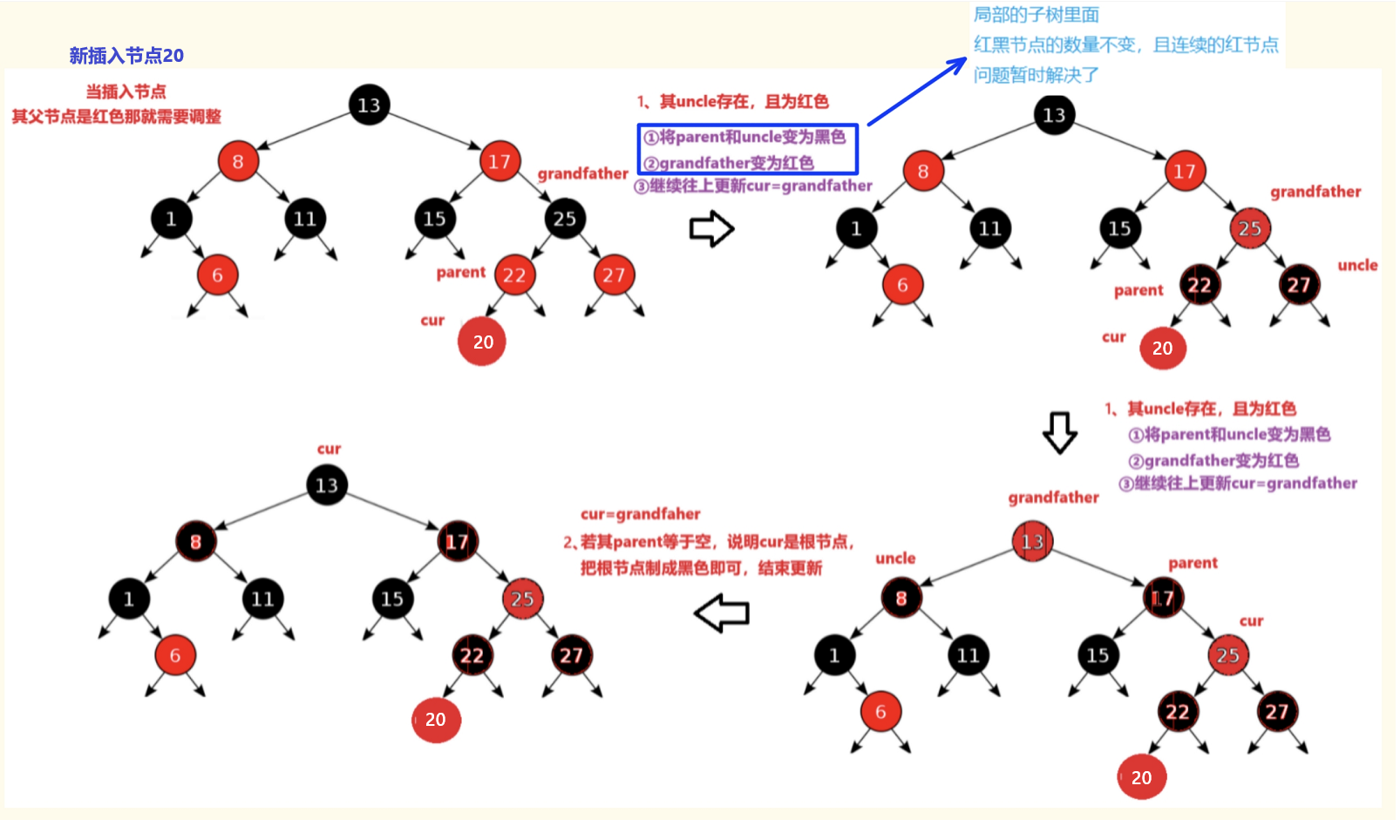
情况二： 当新插入节点其父节点是红色那就需要调整

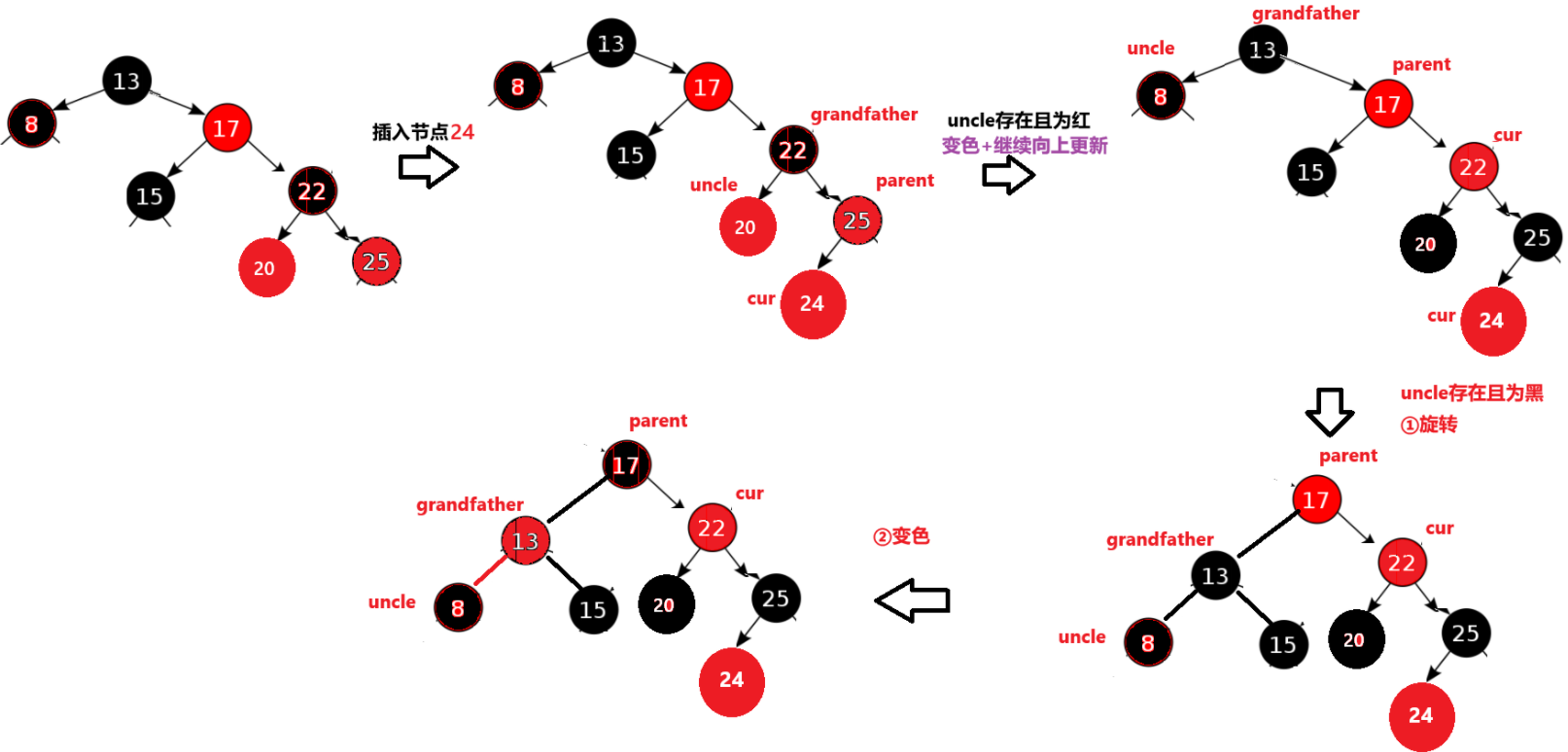
①其uncle存在，且为红色(变色+继续向上更新)

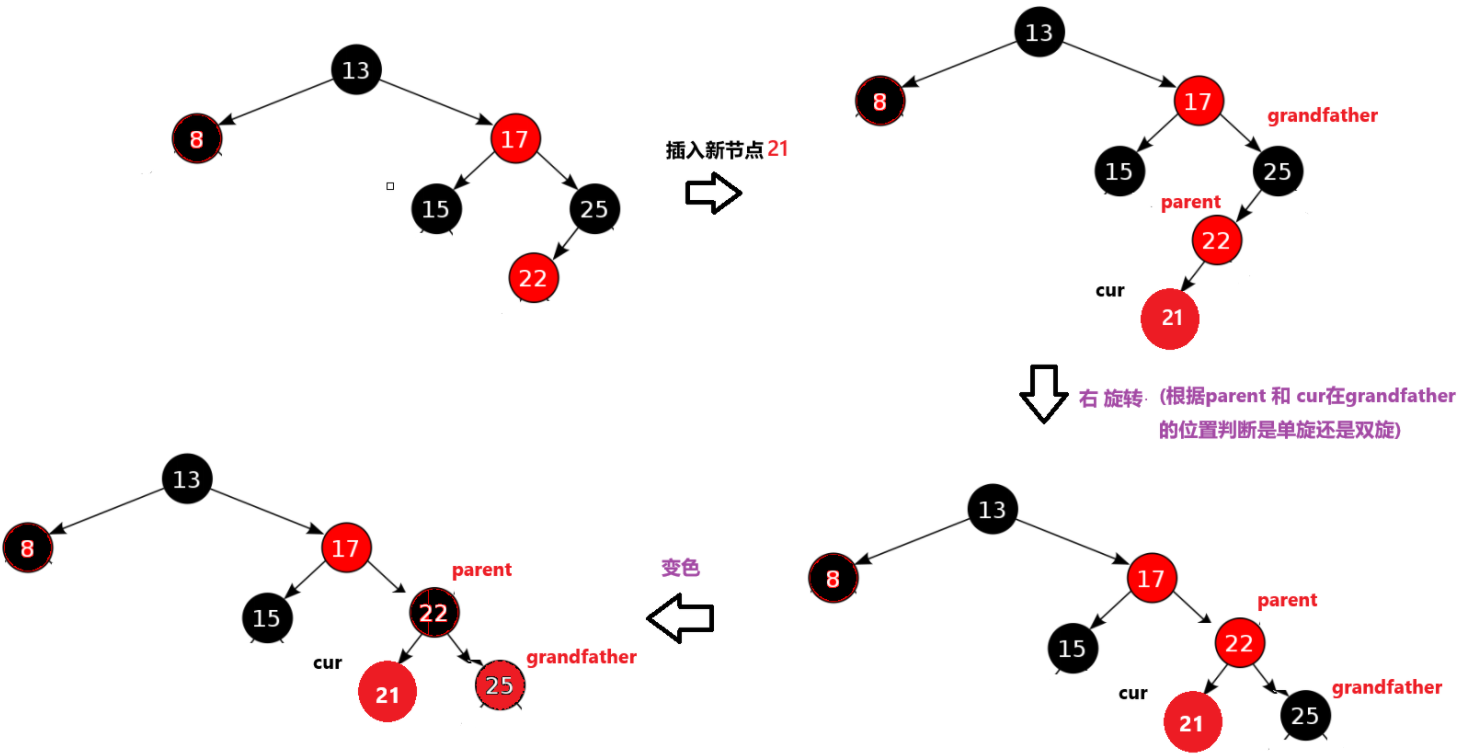
 ②其uncle不存在(旋转+变色)

③其uncle存在且为黑(旋转+变色) 

综合上面需要更新的情况总结：

红黑树插入这么更新关键看uncle

1、uncle存在且为红------ 策略：变色+继续往上更新

2、uncle不存在 ------策略：旋转+继续往上更新

3、uncle存在且为黑------策略：旋转+继续往上更新(这种情况由 第一种情况演变而来) 

 5.红黑树底层结构

enum COLOR
{
	RED,
	BLACK
};
template
struct RBTreeNode
{
	pair _kv;
	RBTreeNode* _left;
	RBTreeNode* _right;
	RBTreeNode* _parent;
	COLOR _color;
	RBTreeNode(const pair& kv)
		:_kv(kv)
		,_left(nullptr)
		,_right(nullptr)
		,_parent(nullptr)
		,_color(COLOR::RED)
	{ }
};
template
class RBTree
{
	typedef RBTreeNode  Node;
 private:
	Node* _root=nullptr;
};
    

6.插入逻辑代码

bool insert(const pair& kv)
{
	//二叉搜索树的插入
	if (_root == nullptr)
	{
		Node* newNode = new Node(kv);
		_root = newNode;
		_root->_color = BLACK;
		return true;
	}
	Node* cur = _root;
	Node* parent = nullptr;
	while (cur)
	{
		if (cur->_kv.first > kv.first)
		{
			parent = cur;
			cur = cur->_left;
		}
		else if (cur->_kv.first _right;
		}
		else
			return false;
	}
	cur = new Node(kv);
	if (parent->_kv.first > cur->_kv.first)
	{
		parent->_left = cur;
	}
	else
	{
		parent->_right = cur;
	}
	cur->_parent = parent;
	//调节颜色
	while (parent && parent->_color == RED)
	{
		Node* grandfather = parent->_parent;
		if (grandfather->_left == parent)
		{
			Node* uncle = grandfather->_right;
			if (uncle && uncle->_color == RED)
			{
				//变色
				parent->_color = uncle->_color = BLACK;
				grandfather->_color = RED;
				//继续向上处理
				cur = grandfather;
				parent = cur->_parent;
			}
			else //(uncle==nullptr || (uncle && uncle->_color==BLACK))
			{
				if (parent->_left == cur)
				{
					//		g
					//    p
					//	c
					RotateR(grandfather); //右旋
					parent->_color = BLACK;
					grandfather->_color = RED;
				}
				else if ( parent->_right == cur)
				{
					//     g
					//   p
					//		c
					RotateL(parent);  //左旋
					RotateR(grandfather); //右旋
					cur->_color = BLACK;
					grandfather->_color = RED;
				}
				else
					assert(false);
				break;
			}
		}
		else //grandfather->_right == parent
		{
			Node* uncle = grandfather->_left;
			if (uncle && uncle->_color == RED)
			{
				//变色
				parent->_color = uncle->_color = BLACK;
				grandfather->_color = RED;
				//继续向上处理
				cur = grandfather;
				parent = cur->_parent;
			}
			else  //uncle不存在/uncle存在且为黑
			{
				
				if ( parent->_right == cur)
				{
					// g
					//	  p
					//       c
					RotateL(grandfather); //左旋
					grandfather->_color = RED;
					parent->_color = BLACK;
				}
				else if (parent->_left == cur)
				{
					// g
					//	  p
					// c
					RotateR(parent); //右旋
					RotateL(grandfather); //左旋
					cur->_color = BLACK;
					grandfather->_color = RED;
				}
				else
					assert(false);
				break;
			}
		}
	}
	_root->_color = BLACK;
	return true;
}
//左旋
void RotateL(Node* parent)
{
	++rotateCount;
	Node* cur = parent->_right;
	Node* curLeft = cur->_left;
	if (curLeft)
		curLeft->_parent = parent;
	parent->_right = curLeft;
	Node* ppNode = parent->_parent;
	parent->_parent = cur;
	cur->_left = parent;
	//修改cur的父亲
	if (ppNode == nullptr)
	{
		cur->_parent = nullptr;
		_root = cur;
	}
	else
	{
		if (ppNode->_left == parent)
			ppNode->_left = cur;
		else
			ppNode->_right = cur;
		cur->_parent = ppNode;
	}
}
//右旋
void RotateR(Node* parent)
{
	++rotateCount;
	Node* cur = parent->_left;
	Node* curRight = cur->_right;
	parent->_left = curRight;
	if (curRight)
		curRight->_parent = parent;
	Node* ppNode = parent->_parent;
	parent->_parent = cur;
	cur->_right = parent;
	//修改cur的父亲
	if (ppNode == nullptr)
	{
		_root = cur;
		cur->_parent = nullptr;
	}
	else
	{
		if (ppNode->_left == parent)
			ppNode->_left = cur;
		else
			ppNode->_right = cur;
		cur->_parent = ppNode;
	}
}

觉得不错的，大家可以点赞+收藏咯