机器学习-决策树

一、概念

        与决策树相关的小知识点：

决策节点--有下一个节点：通过条件判断而进行分支选择的节点。

叶子结点--没有下一个节点：没有子节点的节点，表示最终的决策结果。

决策树深度：所有节点的最大层次数。根节点的层次数定为0，从下面开始每一层子节点层次数增加。

决策树优点：可视化（可通过工具查看决策树） 、可解释能力、对算力要求低（算力最低的是逻辑回归 ）

决策树缺点：容易产生过拟合，因此不要把决策树深度调得太大。

         还有一个比较形象的决策树，如判断动物是否为鸟，这个决策树比较简单，但是前两张图更直观形象：

二、基于信息增益决策树的建立

        信息增益决策树倾向于选择取值较多的属性，在有些情况下这类属性可能不会提供太多有价值的信息，算法只能对描述属性为离散型属性的数据集构造决策树。

2.1信息熵

        信息熵描述的是不确定性。信息熵越大，不确定性越大。信息熵的值越小，则D的纯度越高。 假设样本集合D共有N类，第k类样本所占比例为，则D的信息熵为

2.2信息增益

        息增益是一个统计量，用来描述一个属性区分数据样本的能力。信息增益越大，那么决策树就会越简洁。这里信息增益的程度用信息熵的变化程度来衡量, 信息增益公式：

解释：

• 信息熵 H(Y) ：衡量随机变量 Y 的不确定性，Y 的取值越杂乱、可能性越多样，H(Y) 就越大 。比如抛一枚质地均匀的硬币，结果有正、反两种，不确定性大，信息熵就大；若硬币两面一样，结果确定，信息熵就小。
• 条件熵 H(Y∣X) ：是在已知随机变量 X 的条件下，随机变量 Y 的不确定性 。也就是知道 X 的信息后，Y 还剩的不确定性。
• 信息增益 IG(Y∣X) ： 是信息熵 H(Y) 减去条件熵 H(Y∣X) 。它表示知道 X 的信息后，随机变量 Y 不确定性减少的程度 。因为知道 X 的信息后，Y 的不确定性只会减少或者不变，所以信息增益 IG(Y∣X)=H(Y)−H(Y∣X)≥0 。

  2.3信息增益决策树建立步骤

  （1）数据准备

          明确数据集，其中包含多个特征（属性）列和一个标签（目标）列。例如，对于判断是否购买电脑的数据集，特征可能有年龄、收入、是否学生等，标签是 “是否购买” 。

  （2）计算初始信息熵 H(Y)

          设标签 Y 有 k 种不同取值，每种取值的概率为 pi​（i=1,2,⋯,k ），根据信息熵公式 计算。比如在 “是否购买电脑” 数据集中，“购买” 和 “不购买” 的数量分别为 m 和 n，总样本数为 N=m+n ，那么 p1​=Nm​ （购买的概率）， p2​=Nn​ （不购买的概率），代入公式即可算出 H(Y) 。

  （3）对每个特征计算条件熵 H(Y∣Xj​)

          假设数据集有 n 个特征 X1​,X2​,⋯,Xn​ 。对于特征 Xj​ ：       

  •        设 Xj​ 有 v 种不同取值 xj1​,xj2​,⋯,xjv​ 。

    • 计算在 Xj​=xji​ 条件下，标签 Y 的信息熵 H(Y∣Xj​=xji​) ，计算方式同步骤 2，不过此时是基于 Xj​=xji​ 这个子集中的 Y 取值概率。

    • 再根据每个 xji​ 在数据集中出现的概率 qi​ ，通过 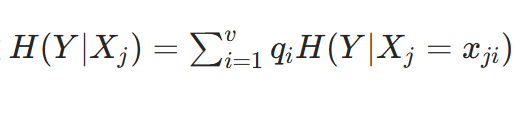计算特征 Xj​ 的条件熵。

      （4） 计算每个特征的信息增益 IG(Y∣Xj​)

              根据信息增益公式 IG(Y∣Xj​)=H(Y)−H(Y∣Xj​) ，分别算出每个特征的信息增益。

      （5）选择划分特征

              选择信息增益最大的特征作为当前节点的划分特征。比如特征 “年龄”“收入”“是否学生” 中，“年龄” 的信息增益最大，就以 “年龄” 来划分数据集。

      （6） 递归构建子树

      • 按照选定的划分特征的不同取值，将数据集划分为多个子集。

      • 对每个子集，重复步骤 2 - 5，继续选择划分特征并划分，直到满足停止条件，如子集中所有样本标签相同（纯度达到 100% ），或者达到预设的树的最大深度、子集中样本数量过少等

        通过以上步骤，就可以基于信息增益逐步构建出一棵决策树。

        2.4案例

        构建决策树：要很快分出类别，深度越简捷越好。

        	职业	年龄	收入	学历	是否贷款
        1	工人	36	5500	高中	否
        2	工人	42	2800	初中	是
        3	白领	45	3300	小学	是
        4	白领	25	10000	本科	是
        5	白领	32	8000	硕士	否
        6	白领	28	13000	博士	是

        计算：

        

        对比属性信息增益发现，"收入"和"学历"相等，并且是最高的，所以我们就可以选择"学历"或"收入"作为第一个决策树的节点， 接下来我们继续重复1，2的做法继续寻找合适的属性节点

         

        三、基于基尼指数决策树的建立

        3.1基尼系数

        3.1.1定义

                基尼指数（Gini Index）是决策树算法中用于评估数据集纯度的一种度量，基尼指数衡量的是数据集的不纯度，或者说分类的不确定性。在构建决策树时，基尼指数被用来决定如何对数据集进行最优划分，以减少不纯度。

        3.1.2计算

              对于一个二分类问题（结果是不是只有两个，如贷款，不贷款），如果一个节点包含的样本属于正类的概率是 (p)，则属于负类的概率是 (1-p)。那么，这个节点的基尼指数 (Gini(p)) 定义为：

        

        对于多分类问题，如果一个节点包含的样本属于第 k 类的概率是 p_k，则节点的基尼指数定义为：

        

        注意：它不同于信息熵，它要用1减。

        3.1.3意义   

        • 当一个节点的所有样本都属于同一类别时，基尼指数为 0，表示纯度最高。（结果为一个类型）

        • 当一个节点的样本均匀分布在所有类别时，基尼指数最大，表示纯度最低。

          3.2基尼系数决策树建立步骤

          1. 数据准备

                  明确数据集，包含多个特征（属性）列和一个标签（目标）列 。例如在判断患者是否患病的医疗数据集中，特征可能有年龄、症状、病史等，标签是 “是否患病” 。

          2. 计算数据集的基尼系数 Gini(D)

                  设数据集 D 中标签有 K 个类别，第 k 个类别样本数为 ∣Ck​∣ ，数据集 D 总样本数为 ∣D∣ ，则基尼系数计算公式为：

          

          比如数据集中 “患病” 样本数为 m ，“不患病” 样本数为 n ，总样本数 N=m+n ，那么 

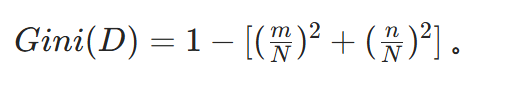
          3. 对每个特征计算划分后的基尼指数 Gini_index(D,A)

          假设数据集有 n 个特征 A1​,A2​,⋯,An​ 。对于特征 A ：

          • 设特征 A 有 v 种不同取值 a1​,a2​,⋯,av​ 。

          • 按照特征 A 的取值将数据集 D 划分为 v 个子集 D1​,D2​,⋯,Dv​ ，第 i 个子集 Di​ 样本数为 ∣Di​∣ ，且 

          • 分别计算每个子集 Di​ 的基尼系数 Gini(Di​) ，计算方式同步骤 2。

          • 再根据每个子集 Di​ 在原数据集 D 中所占比例 ∣D∣∣Di​∣​ ，通过公式 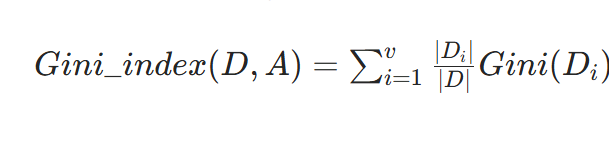计算特征 A 划分后的基尼指数。

            4. 选择划分特征

            选择基尼指数最小的特征作为当前节点的划分特征。比如特征 “年龄”“症状”“病史” 中，“症状” 划分后的基尼指数最小，就以 “症状” 来划分数据集。

            5. 递归构建子树

            • 按照选定的划分特征的不同取值，将数据集划分为多个子集。

            • 对每个子集，重复步骤 2 - 4，继续选择划分特征并划分，直到满足停止条件，如子集中所有样本标签相同（基尼系数为 0 ），或者达到预设的树的最大深度、子集中样本数量过少等 。

              3.3案例

              

               

              

               

              根据基尼指数最小准则， 我们优先选择工资或者平台=0作为D的第一特征。

              我们选择工资作为第一特征，那么当工资=1时，工作=好，无需继续划分。当工资=0时，需要继续划分。

              四、API

                      from sklearn.tree import  DecisionTreeClassifier(criterion，max_depth)

              参数解释：

              criterion :"gini" "entropy” 默认为="gini" 

                  当criterion取值为"gini"时采用 基尼不纯度（Gini impurity）算法构造决策树，

                  当criterion取值为"entropy”时采用信息增益（ information gain）算法构造决策树.

              max_depth :   int, 默认为=None  树的最大深度

                      from sklearn.tree import  export_graphviz(estimator,outaa_file,featrue_names)

              参数解释：

                  estimator决策树预估器

                  out_file生成的文档

                  feature_names节点特征属性名

              五、用决策树对葡萄酒数据集进行分类

              （1）数据加载

              （2）数据划分

              （3）标准化

              （4）决策树预估器

              （5）模型训练

              （6）模型评估

              （7）预测

              （8）可视化决策树

              from sklearn.datasets import load_wine
              from sklearn.model_selection import train_test_split
              from sklearn.preprocessing import StandardScaler
              from sklearn.tree import DecisionTreeClassifier,export_graphviz
              import graphviz
              x,y = load_wine(return_X_y=True)
              x_train,x_test,y_train,y_test = train_test_split(x,y,test_size=0.2,shuffle=True,random_state=44)
              scaler = StandardScaler()
              x_train_s = scaler.fit_transform(x_train)
              x_test_s = scaler.transform(x_test)
              model = DecisionTreeClassifier(criterion='entropy',max_depth=5)
              model.fit(x_train_s,y_train)
              score = model.score(x_test,y_test)
              print('准确度：\n',score)
              y_pred = model.predict(x_test_s)
              print('预测结果：\n',y_pred)
              # 可视化
              export_graphviz(model , out_file="wine_tree.dot", feature_names=load_wine().feature_names)

              结果：

              准确度：

               0.3888888888888889

              预测结果：

               [0 1 0 2 2 0 1 1 0 1 0 0 1 0 1 1 1 0 0 0 0 2 0 0 0 0 2 2 2 1 1 2 1 1 2 0]

              可视化结果需要用图形可视化工具查看：

              digraph Tree {

              node [shape=box, fontname="helvetica"] ;

              edge [fontname="helvetica"] ;

              0 [label="proline