逻辑回归详解:从原理到实践
在机器学习的广阔领域中,逻辑回归(Logistic Regression)虽名为 “回归”,实则是一种用于解决二分类(0 或 1)问题的有监督学习算法。它凭借简单易懂的原理、高效的计算性能以及出色的解释性,在数据科学、医学诊断、金融风控等诸多领域中得到了广泛应用。接下来,我们将从多个维度深入剖析逻辑回归,带你揭开它的神秘面纱。
一、逻辑回归的基本概念
在回归分析中,线性回归是通过构建线性方程来预测连续值,例如根据房屋面积、房间数量等特征预测房价。而逻辑回归面对的是分类问题,比如判断一封邮件是垃圾邮件(1)还是正常邮件(0) 。
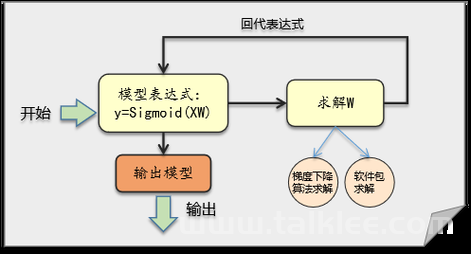
逻辑回归基于线性回归模型,但引入了一个关键的转换函数 ——Sigmoid 函数,将线性回归模型的输出值映射到 [0, 1] 区间,使其能够表示某一事件发生的概率。假设线性回归模型的输出为,其中是参数向量,是特征向量。Sigmoid 函数的表达式为:
g(z)=1+e−z1
Sigmoid 函数的图像呈现出 “S” 型曲线,当
z
趋近于正无穷时,
g(z)
趋近于 1;当
z
趋近于负无穷时,
g(z)
趋近于 0 。将线性回归的输出
z
代入 Sigmoid 函数,得到逻辑回归模型的预测函数:
hθ(x)=g(θTx)=1+e−θTx1
hθ(x)
表示给定特征
x
时,样本属于正类(类别 1)的概率。例如,
hθ(x)=0.8
,则意味着该样本有 80% 的概率属于正类。
二、逻辑回归的数学推导
(一)损失函数
对于线性回归,我们使用均方误差(MSE)作为损失函数来衡量预测值与真实值之间的差异。但在逻辑回归中,由于预测的是概率值,均方误差不再适用,而是采用对数损失函数(Log Loss),也称为交叉熵损失函数(Cross-Entropy Loss)。
假设样本数据集,其中是第个样本的特征向量,是第个样本的真实标签。单个样本的对数损失函数为:
L(hθ(x),y)=−[ylog(hθ(x))+(1−y)log(1−hθ(x))]
当
y=1
时,损失函数简化为
−log(hθ(x))
,此时
hθ(x)
越接近 1,损失越小;当
y=0
时,损失函数变为
−log(1−hθ(x))
,
hθ(x)
越接近 0,损失越小。
整个数据集的对数损失函数(成本函数)为:
J(θ)=−m1i=1∑m[y(i)log(hθ(x(i)))+(1−y(i))log(1−hθ(x(i)))]
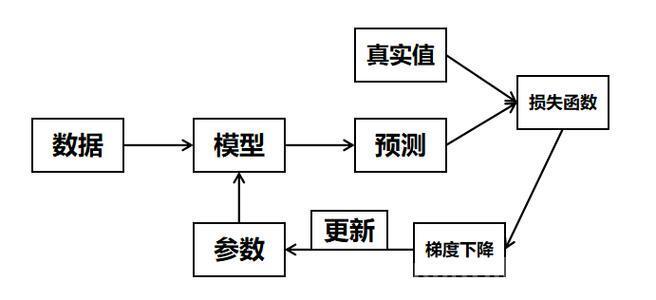
(二)参数优化
逻辑回归的目标是找到一组最优的参数,使得成本函数最小化。通常使用梯度下降法(Gradient Descent)来更新参数。
首先,计算成本函数关于参数的梯度:
∂θj∂J(θ)=m1i=1∑m(hθ(x(i))−y(i))xj(i)
然后,使用梯度下降的更新公式来迭代更新参数
θj
:
θj:=θj−α∂θj∂J(θ)
其中,
α
是学习率,控制每次参数更新的步长。不断重复上述过程,直到成本函数
J(θ)
收敛到最小值或达到预设的迭代次数,此时得到的参数
θ
即为逻辑回归模型的最优参数。
三、逻辑回归的实现步骤
(一)数据预处理
- 数据清洗:检查数据集中是否存在缺失值、异常值,并进行相应处理。例如,对于缺失值可以采用删除含有缺失值的样本、均值填充、中位数填充等方法;对于异常值可以通过统计分析或可视化手段识别并进行修正或删除。
- 特征编码:如果数据集中存在类别型特征,需要将其转换为数值型特征。常用的编码方式有独热编码(One-Hot Encoding)、标签编码(Label Encoding)等 。例如,对于 “颜色” 特征(红、绿、蓝),使用独热编码会将其转换为三个新的特征,每个特征表示一种颜色是否出现(0 或 1)。
- 特征标准化:将特征缩放到相同的尺度,常用的方法有归一化(Min-Max Scaling)和标准化(Z-Score Standardization)。归一化将特征值映射到 [0, 1] 区间,公式为
x′=xmax−xminx−xmin
;标准化将特征值转换为均值为 0,标准差为 1 的分布,公式为x′=σx−μ
,其中μ
是均值,σ
是标准差。
(二)模型训练
在 Python 中,可以使用 Scikit-learn 库方便地实现逻辑回归模型的训练。以下是一个简单的示例代码:
TypeScript
取消自动换行复制
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_iris
import numpy as np
# 加载数据集(这里以鸢尾花数据集为例)
iris = load_iris()
X = iris.data[:, :2] # 选取前两个特征
y = (iris.target == 0).astype(int) # 将类别0作为正类,其他作为负类
# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 创建逻辑回归模型对象
model = LogisticRegression()
# 训练模型
model.fit(X_train, y_train)
(三)模型评估
训练好模型后,需要对其性能进行评估。常用的评估指标有:
- 准确率(Accuracy):表示预测正确的样本数占总样本数的比例,公式为
Accuracy=TP+TN+FP+FNTP+TN
,其中TP
(真正例)是被正确预测为正类的样本数,TN
(真负例)是被正确预测为负类的样本数,FP
(假正例)是被错误预测为正类的样本数,FN
(假负例)是被错误预测为负类的样本数。
- 精确率(Precision):表示预测为正类的样本中真正为正类的比例,公式为
Precision=TP+FPTP
。
- 召回率(Recall):表示实际为正类的样本中被正确预测为正类的比例,公式为
Recall=TP+FNTP
。
- F1 值:是精确率和召回率的调和平均数,公式为
F1=Precision+Recall2×Precision×Recall
。
- ROC 曲线(Receiver Operating Characteristic Curve):以假正率(FPR)为横轴,真正率(TPR)为纵轴绘制的曲线,曲线下面积(AUC,Area Under Curve)越大,模型性能越好。
可以使用 Scikit-learn 库中的相关函数计算这些评估指标,示例代码如下:
TypeScript
取消自动换行复制
from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_score, roc_auc_score, roc_curve
import matplotlib.pyplot as plt
# 预测测试集
y_pred = model.predict(X_test)
# 计算准确率
accuracy = accuracy_score(y_test, y_pred)
print("准确率:", accuracy)
# 计算精确率
precision = precision_score(y_test, y_pred)
print("精确率:", precision)
# 计算召回率
recall = recall_score(y_test, y_pred)
print("召回率:", recall)
# 计算F1值
f1 = f1_score(y_test, y_pred)
print("F1值:", f1)
# 计算ROC曲线和AUC
y_scores = model.predict_proba(X_test)[:, 1] # 得到正类的预测概率
fpr, tpr, thresholds = roc_curve(y_test, y_scores)
auc = roc_auc_score(y_test, y_scores)
# 绘制ROC曲线
plt.plot(fpr, tpr, label='ROC curve (area = %0.2f)' % auc)
plt.plot([0, 1], [0, 1], 'k--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver operating characteristic example')
plt.legend(loc="lower right")
plt.show()
四、逻辑回归的优缺点
(一)优点
- 简单易懂:逻辑回归的原理和模型结构相对简单,容易理解和解释,适合向非技术人员展示模型的决策过程。
- 计算效率高:模型训练和预测的计算复杂度较低,能够快速处理大规模数据集。
- 可解释性强:可以通过参数
θ
的大小和正负来判断每个特征对预测结果的影响方向和程度 。例如,θj>0
表示特征xj
增大时,样本属于正类的概率增加;θj