【C++】红黑树的实现
目录
前言
一、红黑树的概念
二、红黑树的实现
三、红黑树的查找
四、红黑树的验证
五、红黑树的删除
总结
前言
本文讲解红黑树,主要讲解插入部分的实现,建议在理解了AVL树的旋转后再来学习红黑树,因为红黑树也涉及旋转,并且和AVL数的旋转一样。
一、红黑树的概念
1.概念
红黑树是一棵二叉搜索树,他的每个结点增加一个存储位来表示结点的颜色,可以是红色或者黑色。 通过对任何一条从根到叶子的路径上各个结点的颜色进行约束,红黑树确保没有一条路径会比其他路径长出2倍,因而是接近平衡的。
2.红黑树的规则
- 每个结点不是红色就是黑色
- 根节点是黑色的
- 如果一个结点是红色的,则它的两个孩子结点必须是黑色的,也就是说任意一条路径不会有连续的红色结点。
- 对于任意一个结点,从该结点到其所有NULL结点的简单路径上,均包含相同数量的黑色结点。
如下图:
- 以上二叉树都满足红黑树的规则,所以都是属于红黑树。
- 注意:判断红黑树的一条路径是否满足规则时,一定要走到空结点,以空结点为一条路径的终点。比如下图就不是红黑树(最左边路径只有一个黑结点):

- 补充:《算法导论》等书籍上补充了一条每个叶子结点(NIL)都是黑色的规则。他这里所指的叶子结点不是传统的意义上的叶子结点,而是我们说的空结点,有些书籍上也把NIL叫做外部结点。NIL是为了方便准确的标识出所有路径,《算法导论》在后续讲解实现的细节中也忽略了NIL结点,所以我们知道一下这个概念即可。
- 简单来说:上面第3点规则表示红色结点的孩子结点必是黑色,但是该红色结点的孩子可能为空,所以补充说明的意思是空结点也可以看成黑色结点。
- 该补充可以方便我们观察数路径个数,因为每条路径需要数到空结点,我们直接数空结点就行了,但实际代码实现中我们不会去管空结点的颜色的。
如图:
- 红黑树就是通过控制结点颜色以满足以上规则,最终控制整棵树的高度差。
- 总之,通过以上这些规则就能保证:最长路径 _right;
}
else if (kv.first _kv.first)
{
parent = cur;
cur = cur->_left;
}
else
{
return false;//不支持重复节点
}
}
cur = new Node(kv);
if (kv.first > parent->_kv.first)
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
cur->_parent = parent;
//变色
//...
return true;
}
这一段代码相信大家已经很熟悉了,根据搜索二叉树的规则,大的值往右走,小的往左走,直达找到为空的位置插入。
- 2. 如果是空树插,新增结点是黑色结点。如果是非空树插入,新增结点必须红色结点,因为非空树插入,新增黑色结点就破坏了规则4,规则4是很难维护的。
- 具体点说,根节点必须是黑色,因为根节点为红色则孩子节点必为黑,这导致只有1个孩子就破坏了规则4。然后新增节点也必须先设置为红色,因为如果设置为黑色,那么就容易破坏规则4,规则4是每条路径的黑色结点数量相同,所以先设置为红色更合适。
将以上代码加上颜色的初始化:
bool Insert(const pair& kv) { //先按照搜索二叉树的方式查找插入点 if (_root == nullptr) { _root = new Node(kv); _root->_col = BLACK;//根节点为黑色 return true; } Node* cur = _root; Node* parent = nullptr; while (cur) { if (kv.first > cur->_kv.first) { parent = cur; cur = cur->_right; } else if (kv.first _kv.first) { parent = cur; cur = cur->_left; } else { return false; } } cur = new Node(kv); cur->_col = RED;//新增节点为红色 if (kv.first > parent->_kv.first) { parent->_right = cur; } else { parent->_left = cur; } cur->_parent = parent; //变色 //... return true; }剩下步骤:
- 3. 非空树插入后,新增结点必须红色结点,如果父亲结点是黑色的,则没有违反任何规则,插入结束。
- 4. 非空树插入后,新增结点必须红色结点,如果父亲结点是红色的,则违反规则3。需要进一步分析,这时候就需要进行颜色调整了。
说明:上图中假设我们把新增结点x标识为c(cur),c的父亲标识为p(parent),p的父亲标识为 g(grandfather),p的兄弟标识为u(uncle)。
- 根据以上步骤分析,也就是只有检查到父节点为红色时才需要进行调整。
- 如上图新插入节点x的父节点为红色,不符合规则3,也就是红色节点的孩子节点必须为黑色,所以需要调整。
- 我们将新增节点叫c,c的父节点叫p,c的父父节点叫g。仔细分析,如果插入节点时出现父节点为红色的情况,那么这三个节点的颜色是固定的,也就是c、p、g三者颜色固定,唯一不确定的就是c的叔叔节点u了。
- 为什么g一定是黑呢,因为原树肯定需要保持红黑树的,你不能说我插入新节点前你树已经不符合红黑树了,出现问题一定是新增节点时并且在新增节点时解决。
- 所以,调整的关键就是看u的情况,需要根据u分为以下几种情况分别处理。
3.情况1:变色
- 当c为红,p为红,g为黑,u存在且为红时,此时为情况1.
- 解决方法:将p和u变黑,g变红。在把g当做新的c,继续往上更新。
- 分析:因为p和u都是红色,g是黑色,把p和u变黑,左边子树路径各增加一个黑色结点,g再变红,相当于保持g所在子树的黑色结点的数量不变,同时解决了c和p连续红色结点的问题,需要继续往上更新是因为,g是红色,如果g的父亲还是红色,那么就还需要继续处理;如果g的父亲是黑色,则处理结束 了;如果g就是整棵树的根,再把g变回黑色。
- 情况1只变色,不旋转。所以无论c是p的左还是右,p是g的左还是右,都是上面的变色处理方式。
- 和AVL树类似,上图我们展示了一种具体情况,但是实际中需要这样处理的有很多种情况。所以我们使用抽象图表示:

- 如上图将以下类似的处理进行了抽象表达,d、e、f代表每条路径拥有hb个黑色结点的子树,a、b代表每条路径拥有hb-1个黑色结点的根为红的子树(因为x为黑所以hb-1),hb>=0。抽象图中c一开始是黑色,这代表c不是新增节点,c是由于其子树进行了情况1变色,导致自身被修改为红色,需要继续更新。
- 以下是一些具体情况图,随着hb的增加,情况只会更多。(hb为黑色结点的数量)



- 总之,记住情况1只变色不旋转,因此新增节点c无论在p的左边还是右边都可以,p无论在g的左边还是右边无所谓,只要新增节点c的父节点p存在且为红,u也存在且为红,那么就是情况1的变色处理。
可以先将这部分代码写出来:
bool Insert(const pair& kv) { //先按照搜索二叉树的方式查找插入点 if (_root == nullptr) { _root = new Node(kv); _root->_col = BLACK;//根节点为黑色 return true; } Node* cur = _root; Node* parent = nullptr; while (cur) { if (kv.first > cur->_kv.first) { parent = cur; cur = cur->_right; } else if (kv.first _kv.first) { parent = cur; cur = cur->_left; } else { return false; } } cur = new Node(kv); cur->_col = RED;//新增节点为红色 if (kv.first > parent->_kv.first) { parent->_right = cur; } else { parent->_left = cur; } cur->_parent = parent; //红黑树的调整 while (parent && parent->_col == RED)//父节点存在且为红色 { Node* grandfather = parent->_parent;//父父节点 if (grandfather->_left == parent)//parent为左孩子时 { Node* uncle = grandfather->_right;//叔叔节点(父节点的兄弟节点) if (uncle && uncle->_col == RED)//情况1:父节点为红色,叔叔节点也为红色 { //变色 parent->_col = uncle->_col = BLACK;//将父节点和兄弟节点变为黑 grandfather->_col = RED;//父父节点变为红 //继续往上处理 cur = grandfather; parent = cur->_parent; } //其他情况... } else//parent为右孩子,与上面类似,相当于翻个面 { Node* uncle = grandfather->_left;//叔叔节点变为左孩子 if (uncle && uncle->_col == RED)//情况1:父节点为红色,叔叔节点也为红色 { //变色 parent->_col = uncle->_col = BLACK;//将父节点和兄弟节点变为黑 grandfather->_col = RED;//父父节点变为红 //继续往上处理 cur = grandfather; parent = cur->_parent; } //其它情况... } } _root->_col = BLACK;//强制根节点为黑色 return true; }- 简单解释一下,调整的总条件也就是while的条件,就是父节点存在且为红,因为可能需要往上继续调整,所以写成循环。
- 前面说过,情况1对于新增节点的位置不重要,但是因为还有其他情况存在,也就是uncle节点的颜色是红还是黑,这些都涉及需要确认uncle节点,但是拿到uncle节点需要先确认parent节点,所以根据parent是grandfather的左孩子还是右孩子,分成两种情况。
- 这两种情况对于情况1来说,就只有uncle的位置不同了。处理方法就是:只要uncle节点存在且为红,那么就将parent和uncle的颜色改为黑色,grandfather的颜色改为红色,然后因为不确定grandfather的父节点颜色,所以需要继续向上处理。
- 最后因为grandfather可能是根节点,所以无论根节点颜色有没有被改成红色,我们最后都强制根节点为黑色,因为根节点为黑相当于每条路径都至少有一个黑节点,并不违反红黑树的规则。
4.情况2:单旋+变色
- c为红,p为红,g为黑,u不存在或者u存在且为黑,此时属于情况2。
- u不存在,则c一定是新增结点,u存在且为黑,则 c一定不是新增,c之前是黑色的,是在c的子树中插入,符合情况1,变色将c从黑色变成红色,更新上来的。
- 解释:u不存在时,此时只有g一个节点为黑,c不可能是已经存在的黑变为红的,因为u的那条路径只有一个根节点的黑色,所以c为红只能是新增的节点。当u存在且为黑时,c不可能是新增的,因为u为黑,u的那条路径已经有两黑色了,p的那条路径只有1黑,如果c是新增节点,那么说明树之前就不是红黑树了,所以c之前一定是黑色,它是由于其子树出现情况1导致变为红色的。
- 分析:p必须变黑,才能解决,连续红色结点的问题,u不存在或者是黑色时,这里单纯的变色无法解决问题,需要旋转+变色。
- 如上图,u不存在的情况,此时单纯变色解决不了问题,需要进行旋转。
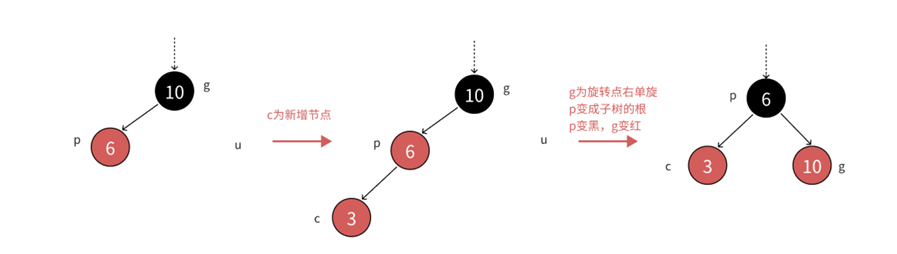
- 根据AVL所学,新增节点到根节点路径为一条直线,只需进行右单旋:将p的右孩子给g的左孩子,再将g变为p的右孩子。
- 单旋后,如图,只需将p的颜色改为黑,g的颜色改为红即可,此时左右路径的黑色数量都相同。
- 最后,请问我们还需要继续往上更新吗?答案是不需要了,无论此时p,c,g是子树还是整棵树,它子树已经平衡不会对外造成影响,所以此时直接break结束就行。
- u存在且为黑时,我们可以看一下抽象图。此时c是已经存在的黑色节点由于子树出现情况1变为的红色,hb是黑色节点数量,a,b一开始是hb-1个,d由于图上只有一个根节点为黑,所以d=hb个,e,f因为已经有两黑色,所以e,f=hb-1。经过右单旋+变色处理后,很明显,加上根节点的黑色后,每条路径都有hb+1个黑色结点。完美的遵循了规则4.
当然,既然是旋转的话,存在右单选,那么肯定存在左单旋,我们将这两种情况总结一下:

- 如上图,如果p是g的左,c是p的左,那么以g为旋转点进行右单旋,再把p变黑,g变红即可。p变成课这颗树新的根,这样子树黑色结点的数量不变,没有连续的红色结点了,且不需要往上更新,因为p的父亲是黑色还是红色或者空都不违反规则。

- 如上,如果p是g的右,c是p的右,那么以g为旋转点进行左单旋,再把p变黑,g变红即可。p变成课这颗树新的根,这样子树黑色结点的数量不变,没有连续的红色结点了,且不需要往上更新,因为p的父亲是黑色还是红色或者空都不违反规则。
代码书写,关于单旋的代码就是将AVL树的单旋拿过来去掉平衡因子部分即可:
public: bool Insert(const pair& kv) { //先按照搜索二叉树的方式查找插入点 if (_root == nullptr) { _root = new Node(kv); _root->_col = BLACK;//根节点为黑色 return true; } Node* cur = _root; Node* parent = nullptr; while (cur) { if (kv.first > cur->_kv.first) { parent = cur; cur = cur->_right; } else if (kv.first _kv.first) { parent = cur; cur = cur->_left; } else { return false; } } cur = new Node(kv); cur->_col = RED;//新增节点为红色 if (kv.first > parent->_kv.first) { parent->_right = cur; } else { parent->_left = cur; } cur->_parent = parent; //红黑树的调整 while (parent && parent->_col == RED)//父节点存在且为红色 { Node* grandfather = parent->_parent;//父父节点 if (grandfather->_left == parent)//parent为左孩子 { Node* uncle = grandfather->_right;//叔叔节点(父节点的兄弟节点) if (uncle && uncle->_col == RED)//情况1:父节点为红色,叔叔节点也为红色 { //变色 parent->_col = uncle->_col = BLACK;//将父节点和兄弟节点变为黑 grandfather->_col = RED;//父父节点变为红 //继续往上处理 cur = grandfather; parent = cur->_parent; } else//情况2:叔叔节点不存在或者存在且为黑,需要旋转+变色 { if (cur == parent->_left)//cur为parent的左孩子 { //形状:此时需要右单旋 // g // p u //c RotateR(grandfather);//右单旋 parent->_col = BLACK; grandfather->_col = RED; } //双旋情况... break; } } else//parent为右孩子,与上面类似,相当于翻个面 { Node* uncle = grandfather->_left;//叔叔节点变为左孩子 if (uncle && uncle->_col == RED)//情况1:父节点为红色,叔叔节点也为红色 { //变色 parent->_col = uncle->_col = BLACK;//将父节点和兄弟节点变为黑 grandfather->_col = RED;//父父节点变为红 //继续往上处理 cur = grandfather; parent = cur->_parent; } else//情况2:叔叔节点不存在或者存在且为黑,需要旋转+变色 { if (cur == parent->_right)//cur为parent的右孩子 { //形状:此时需要左单旋 // g // u p // c RotateL(grandfather);//左单旋 parent->_col = BLACK; grandfather->_col = RED; } //双旋情况... break; } } } _root->_col = BLACK;//强制根节点为黑色 return true; } private: //右单旋 void RotateR(Node* parent) { Node* subL = parent->_left;//左孩子 Node* subLR = subL->_right;//左孩子的右孩子 //旋转过去 parent->_left = subLR; subL->_right = parent; Node* ppNode = parent->_parent;//记录父父节点 //更新父节点指针 if (subLR) subLR->_parent = parent; parent->_parent = subL; if (parent == _root)//判断根节点 { _root = subL; subL->_parent = nullptr; } else { if (ppNode->_left == parent) { ppNode->_left = subL; } else { ppNode->_right = subL; } subL->_parent = ppNode; } } //左单旋 void RotateL(Node* parent) { Node* subR = parent->_right;//右孩子 Node* subRL = subR->_left;//右孩子的左孩子 //旋转过去 parent->_right = subRL; subR->_left = parent; Node* ppNode = parent->_parent;//父父节点 //更新父节点指针 if (subRL) subRL->_parent = parent; parent->_parent = subR; //判断父父节点 if (parent == _root) { _root = subR; subR->_parent = nullptr; } else { if (ppNode->_left == parent) { ppNode->_left = subR; } else { ppNode->_right = subR; } subR->_parent = ppNode; } }代码解释:
- 因为情况1是uncle存在且为红,那么对于情况2就是情况1的相反情况,所以else情况1的if即可,当然,这还只是单旋的情况,只要了解旋转就会知道,是单旋还是双旋是根据新增节点的位置来判断的,所以还需要通过if判断一下c的位置。
- 对于单旋来讲,右单旋:纯粹的左边高,新增节点与根节点的连线为一条直线,此时c在p的左边。左单旋:纯粹的右边高,新增节点与根节点连线也是直线,此时c在p的右边。
- 当然判断c的位置只是判断是双旋还是单旋,我们还需要判断p的位置,来判断是右单旋还是左单旋,很明显c和p都在左边那就是右单旋,c和p都在右边就是左单旋。
- 旋转后,将p变黑,g边红即可,c本来就是红的不用管,最后旋转就不需要继续往上更新了,直接break。
- 关于旋转的代码这里不再详细讲述了,详细请见AVL篇章。
5.情况2:双旋+变色
- 同样都属于情况2,因此前面情况都与单旋一样,c为红,p为红,g为黑,u不存在或者u存在且为黑。u不存在,则c⼀定是新增结点,u存在且为黑,则 c一定不是新增,c之前是黑色的,是在c的子树中插入,符合情况1,变色将c从黑色变成红色,更新上来的。
- 唯一不同的就是新增节点c的位置了,直接明了的说,新增节点到根节点的连线是一条折线,此时需要双旋+变色。
- 如上图,简单的u不存在场景,此时c到g就是一条折线。
- 此时单旋解决不了问题,需要双旋:先以6为根进行左单旋,然后以g为根进行右单旋。

- 最后就是变色:将c变为黑,g变为红,p本来就是红色不用变

- 我们再看一下抽象图,u存在且为黑,c是原来g由黑变为红的,此时c为p的右孩子,折线,需要双旋。
- 双旋:先以p为根节点进行左单旋,将a变为p的右子树,然后将p作为c的左孩子,此时再以g为根进行右单旋,如下图:

- 最后变色就是将c,g变红,p不变。旋转+变色完成后,子树已平衡,不需要继续向上更新。
既然存在左右双旋,那么就存在右左双旋,这里简单总结下:

- 如果p是g的左,c是p的右,那么先以p为旋转点进行左单旋,再以g为旋转点进行右单旋,再把c变黑,g变红即可。c变成这颗树新的根,这样子树黑色结点的数量不变,没有连续的红色结点了,且不需要往上更新,因为c的父亲是黑色还是红色或者空都不违反规则。

- 如果p是g的右,c是p的左,那么先以p为旋转点进行右单旋,再以g为旋转点进行左单旋,再把c变黑,g变红即可。c变成这颗树新的根,这样子树黑色结点的数量不变,没有连续的红色结点了,且不需要往上更新,因为c的父亲是黑色还是红色或者空都不违反规则。
这部分的代码:
//红黑树的调整 while (parent && parent->_col == RED)//父节点存在且为红色 { Node* grandfather = parent->_parent;//父父节点 if (grandfather->_left == parent)//parent为左孩子 { Node* uncle = grandfather->_right;//叔叔节点(父节点的兄弟节点) if (uncle && uncle->_col == RED)//情况1:父节点为红色,叔叔节点也为红色 { //变色 parent->_col = uncle->_col = BLACK;//将父节点和兄弟节点变为黑 grandfather->_col = RED;//父父节点变为红 //继续往上处理 cur = grandfather; parent = cur->_parent; } else//情况2:叔叔节点不存在或者存在且为黑,需要旋转+变色 { if (cur == parent->_left)//cur为parent的左孩子 { //形状:此时需要右单旋 // g // p u //c RotateR(grandfather);//右单旋 parent->_col = BLACK; grandfather->_col = RED; } else//cur为parent的右孩子,需要双旋 { //形状 // g // p u // c RotateL(parent);//先对p进行左单旋 RotateR(grandfather);//再对整体进行右单旋 grandfather->_col = RED; cur->_col = BLACK; } break; } } else//parent为右孩子,与上面类似,相当于翻个面 { Node* uncle = grandfather->_left;//叔叔节点变为左孩子 if (uncle && uncle->_col == RED)//情况1:父节点为红色,叔叔节点也为红色 { //变色 parent->_col = uncle->_col = BLACK;//将父节点和兄弟节点变为黑 grandfather->_col = RED;//父父节点变为红 //继续往上处理 cur = grandfather; parent = cur->_parent; } else//情况2:叔叔节点不存在或者存在且为黑,需要旋转+变色 { if (cur == parent->_right)//cur为parent的右孩子 { //形状:此时需要左单旋 // g // u p // c RotateL(grandfather);//左单旋 parent->_col = BLACK; grandfather->_col = RED; } else//cur为parent的左孩子,需要双旋 { //形状 // g // u p // c RotateR(parent);//先对p进行右单旋 RotateL(grandfather);//再对整体进行左单旋 grandfather->_col = RED; cur->_col = BLACK; } break; } } } _root->_col = BLACK;//强制根节点为黑色- 双旋我们直接使用两个单旋即可,因为没有平衡因子这些东西。
- 剩下的就是更新颜色了,c变黑,g变红。
6.完整的插入代码
public: bool Insert(const pair& kv) { //先按照搜索二叉树的方式查找插入点 if (_root == nullptr) { _root = new Node(kv); _root->_col = BLACK;//根节点为黑色 return true; } Node* cur = _root; Node* parent = nullptr; while (cur) { if (kv.first > cur->_kv.first) { parent = cur; cur = cur->_right; } else if (kv.first _kv.first) { parent = cur; cur = cur->_left; } else { return false; } } cur = new Node(kv); cur->_col = RED;//新增节点为红色 if (kv.first > parent->_kv.first) { parent->_right = cur; } else { parent->_left = cur; } cur->_parent = parent; //红黑树的调整 while (parent && parent->_col == RED)//父节点存在且为红色 { Node* grandfather = parent->_parent;//父父节点 if (grandfather->_left == parent)//parent为左孩子 { Node* uncle = grandfather->_right;//叔叔节点(父节点的兄弟节点) if (uncle && uncle->_col == RED)//情况1:父节点为红色,叔叔节点也为红色 { //变色 parent->_col = uncle->_col = BLACK;//将父节点和兄弟节点变为黑 grandfather->_col = RED;//父父节点变为红 //继续往上处理 cur = grandfather; parent = cur->_parent; } else//情况2:叔叔节点不存在或者存在且为黑,需要旋转+变色 { if (cur == parent->_left)//cur为parent的左孩子 { //形状:此时需要右单旋 // g // p u //c RotateR(grandfather);//右单旋 parent->_col = BLACK; grandfather->_col = RED; } else//cur为parent的右孩子,需要双旋 { //形状 // g // p u // c RotateL(parent);//先对p进行左单旋 RotateR(grandfather);//再对整体进行右单旋 grandfather->_col = RED; cur->_col = BLACK; } break; } } else//parent为右孩子,与上面类似,相当于翻个面 { Node* uncle = grandfather->_left;//叔叔节点变为左孩子 if (uncle && uncle->_col == RED)//情况1:父节点为红色,叔叔节点也为红色 { //变色 parent->_col = uncle->_col = BLACK;//将父节点和兄弟节点变为黑 grandfather->_col = RED;//父父节点变为红 //继续往上处理 cur = grandfather; parent = cur->_parent; } else//情况2:叔叔节点不存在或者存在且为黑,需要旋转+变色 { if (cur == parent->_right)//cur为parent的右孩子 { //形状:此时需要左单旋 // g // u p // c RotateL(grandfather);//左单旋 parent->_col = BLACK; grandfather->_col = RED; } else//cur为parent的左孩子,需要双旋 { //形状 // g // u p // c RotateR(parent);//先对p进行右单旋 RotateL(grandfather);//再对整体进行左单旋 grandfather->_col = RED; cur->_col = BLACK; } break; } } } _root->_col = BLACK;//强制根节点为黑色 return true; } private: //右单旋 void RotateR(Node* parent) { Node* subL = parent->_left;//左孩子 Node* subLR = subL->_right;//左孩子的右孩子 //旋转过去 parent->_left = subLR; subL->_right = parent; Node* ppNode = parent->_parent;//记录父父节点 //更新父节点指针 if (subLR) subLR->_parent = parent; parent->_parent = subL; if (parent == _root)//判断根节点 { _root = subL; subL->_parent = nullptr; } else { if (ppNode->_left == parent) { ppNode->_left = subL; } else { ppNode->_right = subL; } subL->_parent = ppNode; } } //左单旋 void RotateL(Node* parent) { Node* subR = parent->_right;//右孩子 Node* subRL = subR->_left;//右孩子的左孩子 //旋转过去 parent->_right = subRL; subR->_left = parent; Node* ppNode = parent->_parent;//父父节点 //更新父节点指针 if (subRL) subRL->_parent = parent; parent->_parent = subR; //判断父父节点 if (parent == _root) { _root = subR; subR->_parent = nullptr; } else { if (ppNode->_left == parent) { ppNode->_left = subR; } else { ppNode->_right = subR; } subR->_parent = ppNode; } }三、红黑树的查找
查找和二叉搜索树的查找一致
//查找 Node* Find(const K& key) { Node* cur = _root; while (cur) { if (key > cur->_kv.first) { cur = cur->_right; } else if (key _kv.first) { cur = cur->_left; } else { return cur; } } return nullptr; }四、红黑树的验证
和AVL树一样,我们需要验证我们写的插入代码是否正确
这里获取最长路径和最短路径,检查最长路径不超过最短路径的2倍是不可行的,因为就算满足这个条件,红黑树也可能颜色不满足规则,当前暂时没出问题,后续继续插入还是会出问题的。所以我们还是去检查4点规则,满足这4点规则,一定能保证最长路径不超过最短路径的2倍。
- 规则1枚举颜色类型,天然实现保证了颜色不是黑色就是红色。所以无需验证了。
- 规则2直接检查根即可,直接检查根节点是不是黑色。
- 规则3前序遍历检查,遇到红色结点查孩子不太方便,因为孩子有两个,且不一定存在,反过来检查父亲的颜色就方便多了。
- 规则4前序遍历,遍历过程中用形参记录跟到当前结点的blackNum(黑色结点数量),前序遍历遇到黑色结点就++blackNum,走到空就计算出了一条路径的黑色结点数量。再任意一条路径黑色结点数量作为参考值,依次比较即可。
1.IsBalance函数
//判断是否符合红黑树 bool IsBalance() { if (_root == nullptr)//空树也是红黑树 { return true; } if (_root->_col == RED) { return false;//根为红,不用看了 } //统计一条路径的黑色数量,因为每条路径黑色数量应该相等 int refNum = 0; Node* cur = _root; while (cur) { if (cur->_col == BLACK) { ++refNum; } cur = cur->_left; } return Check(_root, 0, refNum); }- IsBalance是我们调用用来验证红黑树正确性的主函数。
- IsBalance先进行简单的排查,如果是空树也是红黑树返回true,如果根节点为红色那么直接返回false,因为违反规则2.
- 然后IsBalance就统计任意一条路径的黑色结点数量,用于后续判断每条路径的黑色结点数量是否相同,也就是规则4。这里我们选择的是最左边的一条路径,循环到底,统计检查到的黑色结点数量,也就是refNum。
- 最后调用Check进行最终的判断。
2.Check函数
//递归检查每一条路径的黑色数量是否正确已经有没有连续红色 bool Check(Node* root, int blackNum, const int refNum) { if (root == nullptr) { //走到空,说明一条路径走完了 if (blackNum != refNum) { cout _parent->_col == RED) { cout _kv.first _left, blackNum, refNum) && Check(root->_right, blackNum, refNum); }- Check是一个递归函数,专门用来检测每条路径是否满足规则3和规则4。
- 参数:root传下一个节点,blackNum是统计当前节点到根节点一共有多少个黑色结点,refNum就是IsBalance函数中统计的一条路径的黑色节点数量。
- 首先检查是否递归到了一条路径的最终结点——空节点,是的话此时就可以判断这条路径的黑色结点数量是否等于refNum了。是就返回true,不是就返回false,并且打印错误提示。
- 然后就是检查规则3了,规则3要求红色节点的孩子节点必须为黑色,这个不太好检查,我们反过来检查红色节点的父节点是不是红色,因为本质都是判断有没有连续的红色节点。如果有连续的红色节点,打印错误信息然后返回false。
- 然后就是统计当前节点到根节点的黑色结点数量,这个只需要记录当前节点即可,然后作为形参传给下一个递归函数。
- 最后,继续递归遍历当前节点孩子节点。最终返回检查结果。(以下是递归示意图)

3.完整的红黑树代码+检测代码
RETree.h
#pragma once #include using namespace std; //用枚举定义红黑颜色 enum Colour { RED, BLACK }; //定义红黑树节点 template struct RBTreeNode { pair _kv;//数据 RBTreeNode* _left;//左孩子指针 RBTreeNode* _right;//右孩子指针 RBTreeNode* _parent;//父结点指针 Colour _col;//颜色 RBTreeNode(const pair& kv) :_kv(kv) , _left(nullptr) , _right(nullptr) ,_parent(nullptr) { } }; //红黑树定义 template class RBTree { typedef RBTreeNode Node;//重命名 public: bool Insert(const pair& kv) { //先按照搜索二叉树的方式查找插入点 if (_root == nullptr) { _root = new Node(kv); _root->_col = BLACK;//根节点为黑色 return true; } Node* cur = _root; Node* parent = nullptr; while (cur) { if (kv.first > cur->_kv.first) { parent = cur; cur = cur->_right; } else if (kv.first _kv.first) { parent = cur; cur = cur->_left; } else { return false; } } cur = new Node(kv); cur->_col = RED;//新增节点为红色 if (kv.first > parent->_kv.first) { parent->_right = cur; } else { parent->_left = cur; } cur->_parent = parent; //红黑树的调整 while (parent && parent->_col == RED)//父节点存在且为红色 { Node* grandfather = parent->_parent;//父父节点 if (grandfather->_left == parent)//parent为左孩子 { Node* uncle = grandfather->_right;//叔叔节点(父节点的兄弟节点) if (uncle && uncle->_col == RED)//情况1:父节点为红色,叔叔节点也为红色 { //变色 parent->_col = uncle->_col = BLACK;//将父节点和兄弟节点变为黑 grandfather->_col = RED;//父父节点变为红 //继续往上处理 cur = grandfather; parent = cur->_parent; } else//情况2:叔叔节点不存在或者存在且为黑,需要旋转+变色 { if (cur == parent->_left)//cur为parent的左孩子 { //形状:此时需要右单旋 // g // p u //c RotateR(grandfather);//右单旋 parent->_col = BLACK; grandfather->_col = RED; } else//cur为parent的右孩子,需要双旋 { //形状 // g // p u // c RotateL(parent);//先对p进行左单旋 RotateR(grandfather);//再对整体进行右单旋 grandfather->_col = RED; cur->_col = BLACK; } break; } } else//parent为右孩子,与上面类似,相当于翻个面 { Node* uncle = grandfather->_left;//叔叔节点变为左孩子 if (uncle && uncle->_col == RED)//情况1:父节点为红色,叔叔节点也为红色 { //变色 parent->_col = uncle->_col = BLACK;//将父节点和兄弟节点变为黑 grandfather->_col = RED;//父父节点变为红 //继续往上处理 cur = grandfather; parent = cur->_parent; } else//情况2:叔叔节点不存在或者存在且为黑,需要旋转+变色 { if (cur == parent->_right)//cur为parent的右孩子 { //形状:此时需要左单旋 // g // u p // c RotateL(grandfather);//左单旋 parent->_col = BLACK; grandfather->_col = RED; } else//cur为parent的左孩子,需要双旋 { //形状 // g // u p // c RotateR(parent);//先对p进行右单旋 RotateL(grandfather);//再对整体进行左单旋 grandfather->_col = RED; cur->_col = BLACK; } break; } } } _root->_col = BLACK;//强制根节点为黑色 return true; } //查找 Node* Find(const K& key) { Node* cur = _root; while (cur) { if (key > cur->_kv.first) { cur = cur->_right; } else if (key _kv.first) { cur = cur->_left; } else { return cur; } } return nullptr; } //判断是否符合红黑树 bool IsBalance() { if (_root == nullptr)//空树也是红黑树 { return true; } if (_root->_col == RED) { return false;//根为红,不用看了 } //统计一条路径的黑色数量,因为每条路径黑色数量应该相等 int refNum = 0; Node* cur = _root; while (cur) { if (cur->_col == BLACK) { ++refNum; } cur = cur->_left; } return Check(_root, 0, refNum); } //中序遍历 void InOrder() { _InOrder(_root); } //计算大小 int Size() { return _Size(_root); } //计算高度 int Height() { return _Height(_root); } private: //递归检查每一条路径的黑色数量是否正确已经有没有连续红色 bool Check(Node* root, int blackNum, const int refNum) { if (root == nullptr) { //走到空,说明一条路径走完了 if (blackNum != refNum) { cout _parent->_col == RED) { cout _kv.first _left, blackNum, refNum) && Check(root->_right, blackNum, refNum); } //右单旋 void RotateR(Node* parent) { Node* subL = parent->_left;//左孩子 Node* subLR = subL->_right;//左孩子的右孩子 //旋转过去 parent->_left = subLR; subL->_right = parent; Node* ppNode = parent->_parent;//记录父父节点 //更新父节点指针 if (subLR) subLR->_parent = parent; parent->_parent = subL; if (parent == _root)//判断根节点 { _root = subL; subL->_parent = nullptr; } else { if (ppNode->_left == parent) { ppNode->_left = subL; } else { ppNode->_right = subL; } subL->_parent = ppNode; } } //左单旋 void RotateL(Node* parent) { Node* subR = parent->_right;//右孩子 Node* subRL = subR->_left;//右孩子的左孩子 //旋转过去 parent->_right = subRL; subR->_left = parent; Node* ppNode = parent->_parent;//父父节点 //更新父节点指针 if (subRL) subRL->_parent = parent; parent->_parent = subR; //判断父父节点 if (parent == _root) { _root = subR; subR->_parent = nullptr; } else { if (ppNode->_left == parent) { ppNode->_left = subR; } else { ppNode->_right = subR; } subR->_parent = ppNode; } } //计算高度 int _Height(Node* root) { if (root == nullptr) return 0; int leftHeight = _Height(root->_left); int rightHeight = _Height(root->_right); return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1; } //计算大小 int _Size(Node* root) { if (root == nullptr) return 0; int left = _Size(root->_left); int right = _Size(root->_right); return left + right + 1; } //中序遍历(左根右) void _InOrder(Node* root) { if (root == nullptr) return; _InOrder(root->_left); cout _kv.first
- u存在且为黑时,我们可以看一下抽象图。此时c是已经存在的黑色节点由于子树出现情况1变为的红色,hb是黑色节点数量,a,b一开始是hb-1个,d由于图上只有一个根节点为黑,所以d=hb个,e,f因为已经有两黑色,所以e,f=hb-1。经过右单旋+变色处理后,很明显,加上根节点的黑色后,每条路径都有hb+1个黑色结点。完美的遵循了规则4.
免责声明:我们致力于保护作者版权,注重分享,被刊用文章因无法核实真实出处,未能及时与作者取得联系,或有版权异议的,请联系管理员,我们会立即处理! 部分文章是来自自研大数据AI进行生成,内容摘自(百度百科,百度知道,头条百科,中国民法典,刑法,牛津词典,新华词典,汉语词典,国家院校,科普平台)等数据,内容仅供学习参考,不准确地方联系删除处理! 图片声明:本站部分配图来自人工智能系统AI生成,觅知网授权图片,PxHere摄影无版权图库和百度,360,搜狗等多加搜索引擎自动关键词搜索配图,如有侵权的图片,请第一时间联系我们。