【人工智能数学基础篇】——深入详解矩阵分解：奇异值分解（SVD）与主成分分析（PCA）在数据降维与特征提取中的应用

目录

1. 引言

2. 矩阵分解概述

2.1 矩阵分解的意义

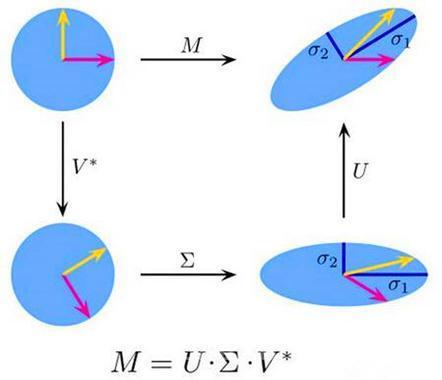
 3. 奇异值分解（SVD）

3.1 定义与数学基础

3.2 SVD 的性质

3.3 SVD 在数据降维中的应用

3.4 示例代码：使用 SVD 进行图像压缩

3.5 结果分析

4. 主成分分析（PCA）

4.1 定义与数学基础

4.2 PCA 与协方差矩阵

4.3 PCA 与 SVD 的关系

4.4 PCA 在特征提取中的应用

4.5 示例代码：使用 PCA 进行手写数字分类

4.6 结果分析

 5. SVD 与 PCA 的比较

6. 其他矩阵分解方法简介

 6.1 LU分解

 6.2 QR分解

 6.3 非负矩阵分解（NMF）

 6.4 矩阵近似

7. 实践中的注意事项

7.1 数据预处理

7.2 选择适当的 \( k \) 值

7.3 处理高维稀疏数据

 7.4 评估降维效果

7.5 扩展方法

8. 结论

 9. 参考资料

1. 引言

        在现代数据分析与机器学习领域，数据的维度通常非常高，这不仅增加了计算复杂度，还可能导致“维度灾难”（Curse of Dimensionality）。为了高效处理和理解高维数据，数据降维与特征提取技术显得尤为重要。矩阵分解作为一种强大的数学工具，在数据降维与特征提取中扮演着关键角色。本文将深入探讨两种经典的矩阵分解方法——奇异值分解（Singular Value Decomposition, SVD）和主成分分析（Principal Component Analysis, PCA），并详细介绍它们在数据降维和特征提取中的应用与实现。

2. 矩阵分解概述

        矩阵分解是将一个复杂的矩阵表示为多个简单矩阵的乘积。不同的分解方法适用于不同的应用场景，能够揭示矩阵的内在结构和特征。常见的矩阵分解方法包括LU分解、QR分解、特征值分解、奇异值分解（SVD）和主成分分析（PCA）等。本文将重点介绍SVD和PCA，并阐述它们在数据降维和特征提取中的应用。