滑膜控制-理论体系架构与核心内容总结
滑模控制理论体系架构与核心内容总结
一、滑模控制理论概述
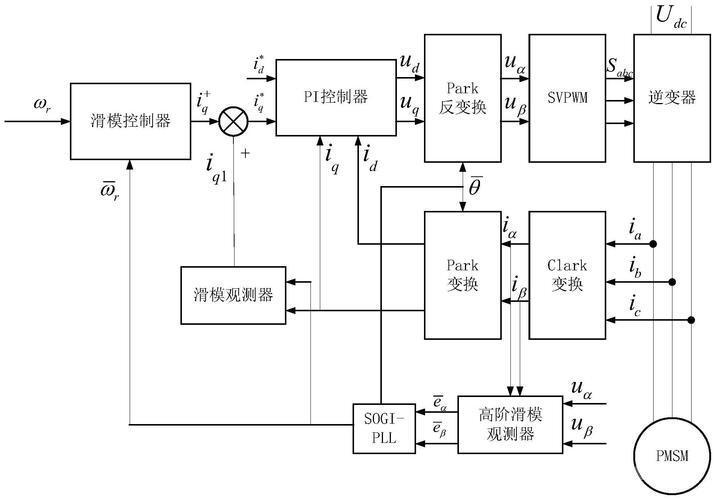
滑模控制(Sliding Mode Control, SMC)作为变结构控制(Variable Structure Control, VSC)的典型代表,通过设计不连续控制律迫使系统状态在特定“滑动模态面”上运动,具有对参数摄动和外部干扰的强鲁棒性。其核心思想是利用控制输入的高频切换(开关特性),使系统沿滑模面作渐近运动,对匹配不确定性(满足匹配条件的干扰)具有完全鲁棒性。自1957年前苏联学者Emelyanov提出以来,滑模控制已广泛应用于机器人、航空航天、电力电子等领域,尤其适用于非线性、强耦合系统。
二、核心章节与关键内容
1. 绪论
- 理论起源:源于对继电控制系统的数学抽象,解决传统控制对不确定性的敏感问题。
- 核心优势:
- 对匹配不确定性的完全鲁棒性(干扰不影响滑模运动)。
- 有限时间收敛(状态在有限时间到达滑模面)。
- 挑战:抖振(Chattering)问题(高频切换引起的控制输入振荡)。
2. 理论基础:滑动模态与稳定性
2.1 滑模面设计
- 滑模面(Switching Surface):
定义为 s ( x ) = C x = 0 s(\mathbf{x}) = \mathbf{Cx} = 0 s(x)=Cx=0(线性系统),其中 C ∈ R 1 × n \mathbf{C} \in \mathbb{R}^{1 \times n} C∈R1×n 为滑模面系数矩阵。
- 设计目标:使滑模运动具有期望动态(如极点配置)。
- 示例(二阶系统):
s
=
e
˙
+
λ
e
(
λ
>
0
)
s = \dot{e} + \lambda e \ (\lambda > 0)
s=e˙+λe (λ>0),保证滑模运动为一阶指数收敛。
2.2 滑动模态存在条件
- 可达性条件(Reachability Condition):
s s ˙ 0)
-
等效控制(单输入系统):
u e q = ( b T C ) − 1 ( − C A x ) u_{eq} = (\mathbf{b}^T\mathbf{C})^{-1}(-\mathbf{C}\mathbf{A}\mathbf{x}) ueq=(bTC)−1(−CAx)
-
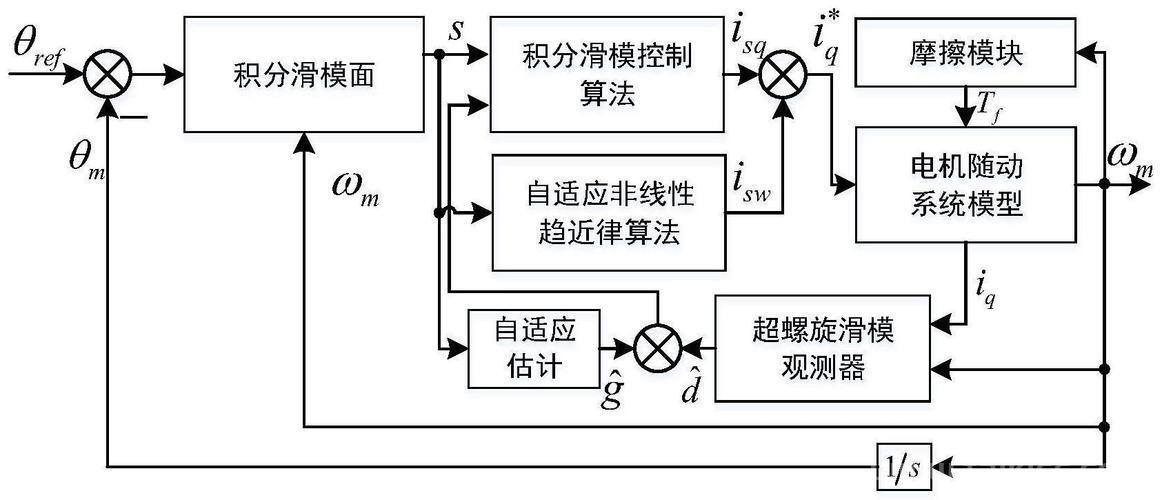
超螺旋算法(二阶滑模):
(图片来源网络,侵删){ s ˙ = − λ ∣ s ∣ 1 / 2 sign ( s ) + σ σ ˙ = − μ ⋅ sign ( s ) ( λ , μ > 0 ) \begin{cases} \dot{s} = -\lambda |s|^{1/2}\text{sign}(s) + \sigma \\ \dot{\sigma} = -\mu \cdot \text{sign}(s) \end{cases} \quad (\lambda, \mu > 0) {s˙=−λ∣s∣1/2sign(s)+σσ˙=−μ⋅sign(s)(λ,μ>0)
2. 核心术语对照
术语 定义 工程意义 滑模面 状态轨迹的“滑动模态”约束(s=0) 决定系统的期望动态 等效控制 滑模面上的连续控制分量 维持滑动模态的标称控制 切换控制 不连续控制分量(如sign函数) 迫使状态到达滑模面的“鲁棒项” 抖振 高频控制振荡(由切换引起) 需抑制的副作用(影响执行器寿命) 匹配条件 不确定性可表示为控制增益的倍数( Δ f = b ξ \Delta f = \mathbf{b}\xi Δf=bξ) 滑模鲁棒性的前提条件 🌟 互动支持 🌟
🔔 博客互动指南:
- 点赞 👍:觉得内容有用?点击底部点赞按钮,你的认可就是创作动力!
- 收藏 ⭐️:点击收藏夹,随时回顾技术干货(建议搭配笔记食用更佳~)
- 关注 🔔:点击博主头像旁「+关注」,第一时间获取最新技术分享!
- 评论 💬:有疑问或建议?欢迎在评论区留言,博主会及时回复交流!
💻 祝福大家:
「愿你的代码没有bug,发际线永远坚挺!」
(图片来源网络,侵删)—— 致敬每一位在0和1的世界里创造奇迹的开发者!
🌈 关于博主:
专注「控制理论」[linux系统]「嵌入式系统」「AI」领域,定期分享技术干货与项目实战。
(图片来源网络,侵删)
- 可达性条件(Reachability Condition):
- 滑模面(Switching Surface):