【统计02】单因素方差分析(One-way ANOVA)与双因素方差分析(Two-way ANOVA)的SPSS/GraphPad实操
本文将详细介绍单因素方差分析(One-way ANOVA)和双因素方差分析(Two-way ANOVA)的SPSS和GraphPad实操步骤,帮助大家更好地理解和应用这两种方法。
一、单因素方差分析(One-way ANOVA)
1. GraphPad实操步骤
数据输入:在GraphPad中创建一个新的项目,选择“Column”(列)数据表,输入因变量和自变量的数据。以上一篇的数据为例:
-
选择分析方法:点击“Analyze”(分析)> “One-way ANOVA”(单因素方差分析)。
设置变量:在弹出的对话框中,选择因变量和自变量,设置好相关参数。
多重比较:直接点确定的单因素方差分析得出的结果只能知道整体的变量X是否有影响,实际应用中,我们一般需要知道某两组之间的数据是否有显著性差异,所以我们要在勾选多重比较。
运行分析:点击“OK”(确定),GraphPad将输出单因素方差分析的结果,包括ANOVA表和事后检验结果。
2. SPSS实操步骤
-
数据输入:在SPSS中输入数据,第一列为因变量(如成绩),第二列为自变量(如组别)。
-
选择分析方法:点击菜单栏的“Analyze”(分析)> “Compare Means”(比较均值)> “One-Way ANOVA”(单因素方差分析)。
-
设置变量:在弹出的对话框中,将因变量(如成绩)拖到“Dependent List”(因变量列表)中,将自变量(如组别)拖到“Factor”(因素)中。
-
选项设置:点击“Options”(选项),选择“Descriptive”(描述统计)和“Homogeneity of Variance”(方差齐性检验),然后点击“Continue”(继续)。
-
事后检验:点击“Post Hoc”(事后检验),选择“Tukey”(图基检验)或其他检验方法,然后点击“Continue”(继续)。
-
运行分析:点击“OK”(确定),SPSS将输出单因素方差分析的结果,包括描述统计、方差齐性检验和ANOVA表。
二、双因素方差分析(Two-way ANOVA)
3. GraphPad实操步骤
-
数据输入:在GraphPad中创建一个新的项目,选择“Column”(列)数据表,输入因变量和两个自变量的数据。
-
选择分析方法:点击“Analyze”(分析)> “Two-way ANOVA”(双因素方差分析)。
-
设置变量:在弹出的对话框中,选择因变量和两个自变量,设置好相关参数。
-
运行分析:点击“OK”(确定),GraphPad将输出双因素方差分析的结果,包括ANOVA表和效应量。
2. SPSS实操步骤
-
数据输入:在SPSS中输入数据,包括因变量和两个自变量。
-
选择分析方法:点击菜单栏的“Analyze”(分析)> “General Linear Model”(一般线性模型)> “Univariate”(单变量)。
-
设置变量:在弹出的对话框中,将因变量拖到“Dependent Variable”(因变量)中,将两个自变量拖到“Fixed Factors”(固定因素)中。
-
模型设置:点击“Model”(模型),选择“Custom”(自定义),将两个自变量及其交互作用项添加到模型中。
-
选项设置:点击“Options”(选项),选择“Descriptive statistics”(描述统计)和“Estimates of effect size”(效应量估计),然后点击“Continue”(继续)。
-
运行分析:点击“OK”(确定),SPSS将输出双因素方差分析的结果,包括ANOVA表和效应量。
三、结果解读
1. ANOVA表
ANOVA表中包含以下几个关键部分:
-
Sum of Squares (SS):平方和,表示数据的总变异。
-
Degrees of Freedom (df):自由度,表示数据的独立性。
-
Mean Square (MS):均方,表示变异的平均值。
-
F值:F统计量,表示组间变异与组内变异的比值。
-
p值:显著性水平,表示结果的显著性。
2. 结果判断
-
p值
-
p值 ≥ 0.05:表示结果不具有统计学意义,接受原假设,认为不同组之间不存在显著差异。
以上一篇的数据做的one way ANOVA为例:
首先看方差分析结果:
1. 关注P值,判断是否有显著性
2.关注F值,一般文献中需要报道
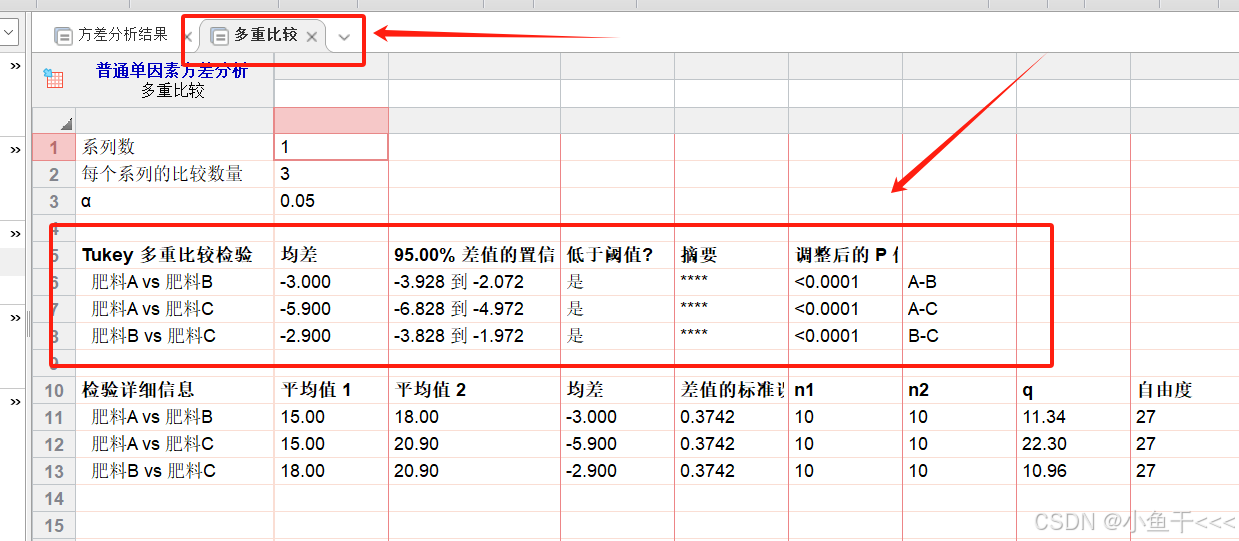
然后看多重比较的结果:
每组之间是否有显著差异一目了然
四、注意事项
1. 数据正态性
在进行ANOVA分析之前,需要检验数据是否符合正态分布。可以使用Shapiro-Wilk检验或Kolmogorov-Smirnov检验。
2. 方差齐性
ANOVA假设各组数据的方差相等。可以使用Levene检验或Bartlett检验来检验方差齐性。
3. 事后检验
如果ANOVA结果显示存在显著差异,需要进行事后检验(如Tukey检验、Bonferroni检验)来确定具体哪些组之间存在差异。
-